Question

【題目】如圖，四棱錐P﹣ABCD中，底面ABCD是邊長為2的菱形，∠DAB＝60°，AC∩BD＝O，點P在底面的射影為點O，PO＝3，點E為線段PD中點．

（1）求證：PB∥平面AEC；

（2）若點F為側棱PA上的一點，當PA⊥平面BDF時，試確定點F的位置，并求出此時幾何體F﹣BDC的體積．

Answer 1

【答案】（1）見解析（2）F為AP的四等分點（靠近A），幾何體F﹣BDC的體積為

【解析】

（1）連接OE，利用中位線知識即可證得：PB∥OE，問題得證。

（2）利用PO⊥平面ABCD證得：BD⊥PA，作BF⊥PA交PA于F，連接DF，即可證得：PA⊥平面BDF，利用等面積法可得OF，結合已知可得：F為AP的四等分點（靠近A），利用體積轉化可得：VF﹣BDC，再利用錐體體積公式計算得解。

解：

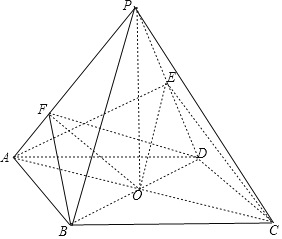
（1）證明：連接OE，

∵O，E為BD，PD的中點，

∴PB∥OE，

又PB平面AEC，OE平面AEC，

∴PB∥平面AEC；

（2）∵PO⊥平面ABCD，

∴PO⊥BD，

又BD⊥AC，

∴BD⊥平面PAC，

∴BD⊥PA，

作BF⊥PA交PA于F，連接DF，

則PA⊥平面BDF，

在菱形ABCD中，∠DAB＝60°，邊長為2，

可求得AO，

在Rt△POA中，求得PA，

連接OF，易知PA⊥OF，

利用等面積法可得OF，

在Rt△AFO中，求得AF，

即F為AP的四等分點（靠近A），

∴VF﹣BDC

．

故幾何體F﹣BDC的體積為．