
【題目】已知等差數列![]() 中,公差
中,公差![]() ,其前
,其前![]() 項和為
項和為![]() ,且滿足:
,且滿足:![]() .
.
(Ⅰ)求數列![]() 的通項公式;
的通項公式;
(Ⅱ)通過公式![]() 構造一個新的數列
構造一個新的數列![]() .若
.若![]() 也是等差數列,求非零常數
也是等差數列,求非零常數![]() ;
;
(Ⅲ)求![]() 的最大值.
的最大值.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)
;(III)![]()
【解析】
試題
(1)由等差數列的性質可得a2+a3=14,解方程組可得a2=5,a3=9,于是可求得首項和公差,從而可得通項公式.(2)由題意得Sn=2n2-n,故![]() ,根據數列為等差數列可得2b2=b1+b3,計算可得
,根據數列為等差數列可得2b2=b1+b3,計算可得![]() .經驗證可得
.經驗證可得![]() 滿足題意.(3)由(2)可得
滿足題意.(3)由(2)可得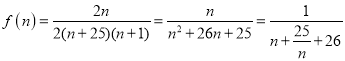 ,故可根據基本不等式求最值.
,故可根據基本不等式求最值.
試題解析:
(1)∵數列{an}是等差數列.
∴a2+a3=a1+a4=14,
由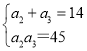 ,解得
,解得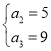 或
或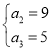 .
.
∵公差d>0,
∴a2=5,a3=9.
∴d=a3-a2=4,a1=a2-d=1.
∴![]() .
.
(2)∵Sn=na1+![]() n(n-1)d=n+2n(n-1)=2n2-n,
n(n-1)d=n+2n(n-1)=2n2-n,
∴![]() .
.
∵數列{bn}是等差數列,
∴2b2=b1+b3,
∴2·![]() =
=![]() +
+![]() ,
,
解得![]() (c=0舍去).
(c=0舍去).
∴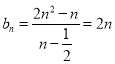 .
.
顯然{bn}成等差數列,符合題意,
∴![]() .
.
(3)由(2)可得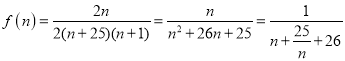
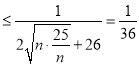 ,當且僅當
,當且僅當![]() ,即
,即![]() 時等號成立.
時等號成立.
∴f(n)的最大值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,四邊形ABCD是矩形,E,M分別是AD,PD的中點,PE⊥BE,PA=PD=AD=2,AB=![]() .
.
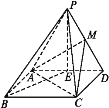
(1)求證:PB∥平面MAC.
(2)求證:平面MAC⊥平面PBE.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】交通管理部門為了解機動車駕駛員(簡稱駕駛員)對某新法規的知曉情況,對甲、乙、丙、丁四個社區做分層抽樣調查.假設四個社區駕駛員的總人數為N,其中甲社區有駕駛員96人.若在甲、乙、丙、丁四個社區抽取駕駛員的人數分別為12,21,25,43,則這四個社區駕駛員的總人數N為( )
A.101
B.808
C.1212
D.2012
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等比數列![]() 的前
的前![]() 項和為
項和為![]() ,公比
,公比![]() ,
,![]() ,
,![]() .
.
(1)求等比數列![]() 的通項公式;
的通項公式;
(2)設![]() ,求
,求![]() 的前
的前![]() 項和
項和![]() .
.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)將已知兩式作差,利用等比數列的通項公式,可得公比,由等比數列的求和可得首項,進而得到所求通項公式;(2)求得bn=n,![]() ,由裂項相消求和可得答案.
,由裂項相消求和可得答案.
(1)等比數列![]() 的前
的前![]() 項和為
項和為![]() ,公比
,公比![]() ,
,![]() ①,
①,
![]() ②.
②.
②﹣①,得![]() ,則
,則![]() ,
,
又![]() ,所以
,所以![]() ,
,
因為![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() ;
;
(2)![]() ,
,![]()
所以前![]() 項和
項和![]() .
.
【點睛】
裂項相消法適用于形如 (其中
(其中![]() 是各項均不為零的等差數列,c為常數)的數列. 裂項相消法求和,常見的有相鄰兩項的裂項求和,還有一類隔一項的裂項求和,如
是各項均不為零的等差數列,c為常數)的數列. 裂項相消法求和,常見的有相鄰兩項的裂項求和,還有一類隔一項的裂項求和,如![]() 或
或![]() .
.
【題型】解答題
【結束】
22
【題目】已知函數![]() 的圖象上有兩點
的圖象上有兩點![]() ,
,![]() .函數
.函數![]() 滿足
滿足![]() ,且
,且![]() .
.
(1)求證:![]() ;
;
(2)求證:![]() ;
;
(3)能否保證![]() 和
和![]() 中至少有一個為正數?請證明你的結論.
中至少有一個為正數?請證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某險種的基本保費為![]() (單位:元),繼續購買該險種的投保人稱為續保人,續保人的本年度的保費與其上年度的出險次數的關聯如下:
(單位:元),繼續購買該險種的投保人稱為續保人,續保人的本年度的保費與其上年度的出險次數的關聯如下:
上年度出險次數 | 0 | 1 | 2 | 3 | 4 |
|
保費 |
|
|
|
|
|
|
設該險種一續保人一年內出險次數與相應概率如下:
一年內出險次數 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(Ⅰ)求一續保人本年度的保費高于基本保費的概率;
(Ⅱ)若一續保人本年度的保費高于基本保費,求其保費比基本保費高出![]() 的概率;
的概率;
(Ⅲ)求續保人本年度的平均保費與基本保費的比值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列兩個命題:命題p1:a,b∈(0,+∞),當a+b=1時, ![]() +
+ ![]() =4;命題p2:函數y=ln
=4;命題p2:函數y=ln ![]() 是偶函數.則下列命題是真命題的是( )
是偶函數.則下列命題是真命題的是( )
A.p1∧p2
B.p1∧(¬p2)
C.(¬p1)∨p2
D.(¬p1)∨(¬p2)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一段時間內,分5次測得某種商品的價格x(萬元)和需求量y(t)之間的一組數據為:
1 | 2 | 3 | 4 | 5 | |
價格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量y | 12 | 10 | 7 | 5 | 3 |
已知![]() ,
,
(1)畫出散點圖;
(2)求出y對x的線性回歸方程;
(3)如價格定為1.9萬元,預測需求量大約是多少?(精確到0.01 t).
參考公式:
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,底面ABCD是邊長為2的菱形,∠DAB=60°,AC∩BD=O,點P在底面的射影為點O,PO=3,點E為線段PD中點.

(1)求證:PB∥平面AEC;
(2)若點F為側棱PA上的一點,當PA⊥平面BDF時,試確定點F的位置,并求出此時幾何體F﹣BDC的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某顏料公司生產A,B兩種產品,其中生產每噸A產品,需要甲染料1噸,乙染料4噸,丙染料2噸,生產每噸B產品,需要甲染料1噸,乙染料0噸,丙染料5噸,且該公司一條之內甲、乙、丙三種染料的用量分別不超過50噸、160噸和200噸,如果A產品的利潤為300元/噸,B產品的利潤為200元/噸,則該顏料公司一天之內可獲得的最大利潤為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com