
科目: 來源: 題型:
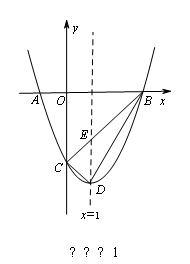
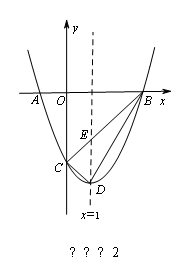
如圖,在平面直角坐標系中,拋物線y=ax2+bx+c的圖象與x軸交于A、B兩點(點A在點B的左邊),與y軸交于點C,點A、C的坐標分別為(﹣1,0),(0,﹣3),直線x=1為拋物線的對稱軸,點D為拋物線的頂點,直線BC與對稱軸相交于點E.
(1)求拋物線的解析式并直接寫出點D 的坐標;
的坐標;
(2)點P為直線x=1右方拋物線上的 一點(點P不與點B重合),記A、B、C、P四點所構成的四邊形面積為
一點(點P不與點B重合),記A、B、C、P四點所構成的四邊形面積為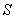 ,若
,若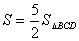 ,求點P的坐標;
,求點P的坐標;
(3)點Q是線段BD上的動點,將△DEQ沿邊EQ翻折得到△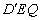 ,是否存在點Q使得△
,是否存在點Q使得△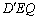 與△BEQ的重疊部分圖形為直角三角形,若存在,請求出BQ的長,若不存在,請說明理由.
與△BEQ的重疊部分圖形為直角三角形,若存在,請求出BQ的長,若不存在,請說明理由.

查看答案和解析>>
科目: 來源: 題型:
如圖,在菱形ABCD中,∠ABC=60°,E是對角線AC上任意一點,F是線段BC延長線上一點,且CF=AE,連接BE、EF.
(1)如圖1,當E是線段AC的中點,且AB=2時,求△ABC的面積;
(2)如圖2,當點E不是線段AC的中點時,求證:BE=EF;
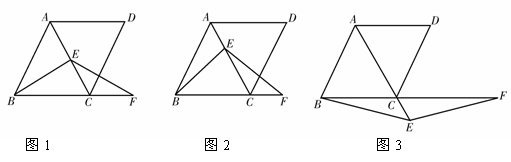 (3)如圖3,當點E是線段AC延長線上的任意一點時,(2)中的結論是否成立?若成立,請給予證明;若不成立,請說明理由.
(3)如圖3,當點E是線段AC延長線上的任意一點時,(2)中的結論是否成立?若成立,請給予證明;若不成立,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
我們對多項式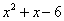 進行因式分解時,可以用待定系數法求解.例如,我們可以先設
進行因式分解時,可以用待定系數法求解.例如,我們可以先設 ,顯然這是一個恒等式.根據多項式乘法將等式右邊展開有:
,顯然這是一個恒等式.根據多項式乘法將等式右邊展開有: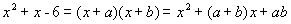
所以,根據等 式兩邊對應項的系數相等,可得:
式兩邊對應項的系數相等,可得: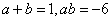 ,解得
,解得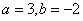 或者
或者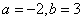 .所以
.所以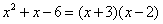 .當然這也說明多項式
.當然這也說明多項式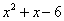 含有因式:
含有因式: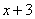 和
和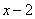 .
.
像上面這種通過利用恒等式的性質來求未知數的方法叫做待定系數法.
利用上述材料及示例解決以下問題.
(1)已知關于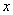 的多項式
的多項式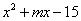 有一個因式為
有一個因式為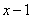 ,求
,求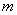 的值;
的值;
(2)已知關于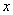 的多項式
的多項式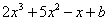 有一個因式為
有一個因式為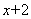 ,求
,求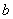 的值.
的值.
查看答案和解析>>
科目: 來源: 題型:
某文具店去年8月底購進了一批文具1160件,預計在9月份進行試銷,購進價格為每件10元.若售價為12元/件,則可全部售出,若每漲價0.1元,銷售量就減少2件.
(1)求該文具店在9月份銷售量不低于1100件,則售價應不高于多少元?
(2)由于銷量好,10月份該文具進價比8月底的進價每件增加20%,該店主增加了進貨量,并加強了宣傳力度,結果10月份的銷售量比9月份在(1)的條件下的最低銷售量增加了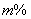 ,但售價比9月份在(1)的條件下的最高售價減少
,但售價比9月份在(1)的條件下的最高售價減少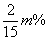 .結果10月份利潤達到3388元,求
.結果10月份利潤達到3388元,求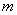 的值(
的值(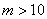 ).
).
查看答案和解析>>
科目: 來源: 題型:
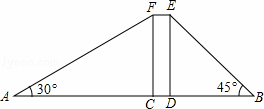
賓哥和君哥在華潤廣場前感慨樓房真高.君哥說:“這樓起碼20層!”賓哥卻不以為然:“20層?我看沒有,數數就知道了!”君哥說:“老大,你有辦法不用數就知道嗎?”賓哥想了想說:“沒問題!讓我們來量一量吧!”君哥、賓哥在樓體兩側各選A、B兩點,其中矩形CDEF表示樓體,AB=200米,CD=20米,∠A=30°,∠B=45°,(A、C、D、B四點在同一直線上)問:
(1)樓高多少米?(用含根號的式子表示)
(2)若每層樓按3米計算,你支持賓哥還是君哥的觀點呢?請說明理由.(精確到0.1,參考數據: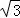 ≈1.73,
≈1.73,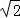 ≈1.41,
≈1.41,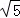 ≈2.24)
≈2.24)
查看答案和解析>>
科目: 來源: 題型:
2015年3月30日至5月11日,我校舉辦了以“讀城 記”為主題的校讀書節暨文化藝術節.為了解初中學生更喜歡下列A、B、C、D哪個比賽,從初中學生中隨機抽取了部分學生進行調查,每個參與調查的學生只選擇最喜歡的一個項目,并將調查結果繪制了兩幅不完整的統計圖,請回答下列問題:
記”為主題的校讀書節暨文化藝術節.為了解初中學生更喜歡下列A、B、C、D哪個比賽,從初中學生中隨機抽取了部分學生進行調查,每個參與調查的學生只選擇最喜歡的一個項目,并將調查結果繪制了兩幅不完整的統計圖,請回答下列問題:
A. “尋找星主播” 校園主持人大賽 B.“育才音超”校園歌手大賽
C.閱讀之星評選 D.“超級演說家”演講比賽
(1)這次被調查的學生共有 人,請你將統計圖1補充完整.
(2)在此調查中,抽到了初一(1)班3人,其中2人喜歡“育才音超”校園歌手大賽、
1人喜歡閱讀之星評選.抽到了初二(5)班2人,其中1人喜歡“超級演說家”演講比賽、1人喜歡閱讀之星評選.從這5人中隨機選兩人,用列表或畫樹狀圖求出兩人都喜歡閱讀之星評選的概率.
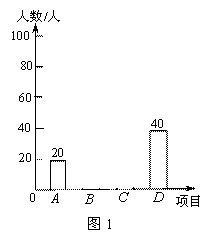 | |||
 | |||
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com