
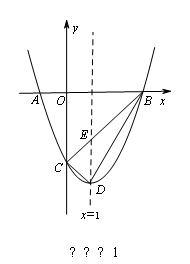
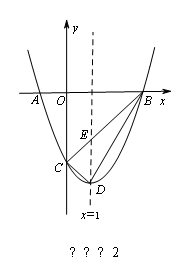
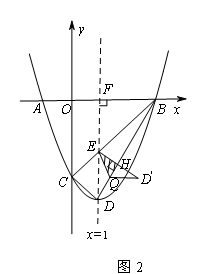
如圖,在平面直角坐標系中,拋物線y=ax2+bx+c的圖象與x軸交于A、B兩點(點A在點B的左邊),與y軸交于點C,點A、C的坐標分別為(﹣1,0),(0,﹣3),直線x=1為拋物線的對稱軸,點D為拋物線的頂點,直線BC與對稱軸相交于點E.
(1)求拋物線的解析式并直接寫出點D 的坐標;
的坐標;
(2)點P為直線x=1右方拋物線上的 一點(點P不與點B重合),記A、B、C、P四點所構(gòu)成的四邊形面積為
一點(點P不與點B重合),記A、B、C、P四點所構(gòu)成的四邊形面積為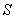 ,若
,若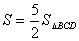 ,求點P的坐標;
,求點P的坐標;
(3)點Q是線段BD上的動點,將△DEQ沿邊EQ翻折得到△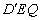 ,是否存在點Q使得△
,是否存在點Q使得△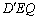 與△BEQ的重疊部分圖形為直角三角形,若存在,請求出BQ的長,若不存在,請說明理由.
與△BEQ的重疊部分圖形為直角三角形,若存在,請求出BQ的長,若不存在,請說明理由.

解:(1)由拋物線的對稱軸直線x=1,A(﹣1,0)可知B(3,0),
設(shè)拋物線y=a(x+1)(x﹣3),將C(0,﹣3)代入得:﹣3=﹣3a,即a=1,
∴拋物線的解析式為:y=x2﹣2x﹣3,其頂點D坐標為:(1,﹣4).
(2)設(shè)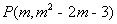 ,易知直線
,易知直線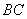 的解析式為:
的解析式為: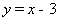 ,令
,令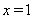 ,則
,則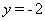 ,所以
,所以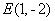 ,
,
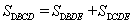
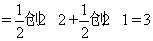
(ⅰ)當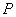 在軸的下方時,即
在軸的下方時,即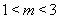 ,連結(jié)
,連結(jié) ,
,
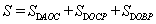
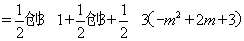
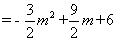
因為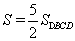 ,則
,則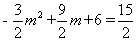 ,
,
化簡得,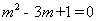 ,解之得
,解之得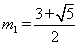 ,
,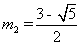 (舍)
(舍)
所以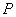 的坐標為
的坐標為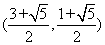
(ⅱ)當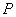 在軸的上方時,即
在軸的上方時,即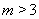 ,
,
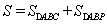
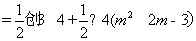
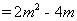
因為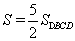 ,則
,則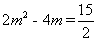 ,
,
化簡得,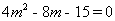 ,解之得
,解之得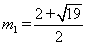 ,
,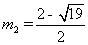 (舍)
(舍)
所以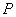 的坐標為
的坐標為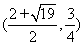
綜上所述,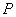 的坐標為
的坐標為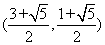 或
或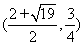 ;
;
(3)存在.(ⅰ)如圖1所示,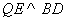 交
交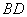 于點
于點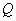 ,∵
,∵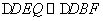 ,
,
∴ 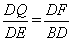 ,即
,即
∴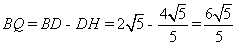 ;
;
(ⅱ)如圖2所示,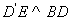 交
交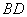 于點
于點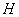 ,∵
,∵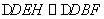 ,
,
∴ 
 ,即
,即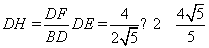 ,同理
,同理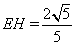
∴ 在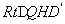 中,設(shè)
中,設(shè)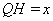 ,由勾股定理得:
,由勾股定理得: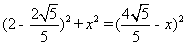 ,解之得
,解之得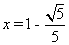 ,
,
∴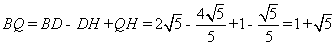 ;
;
(ⅲ)如圖3所示,過點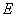 作
作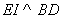 交
交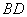 于點
于點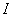 ,由(ⅰ)(ⅱ)可知
,由(ⅰ)(ⅱ)可知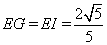 ,
,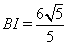
∵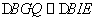 ,
,
∴ 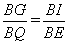 ,即
,即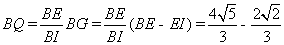 ,
,

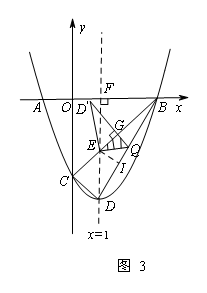 綜上所述,存在點Q使得△D’EQ與△BEQ的重疊部分圖形為直角三角形,
綜上所述,存在點Q使得△D’EQ與△BEQ的重疊部分圖形為直角三角形, 的長度為
的長度為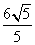 或
或 或
或 .
.


科目:初中數(shù)學(xué) 來源: 題型:
某校 7 名初中男生參加引體向上體育測試的成績分別為:8,5,7,5,8,6,8,則這組數(shù)據(jù)的眾數(shù)和中位數(shù)分別為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
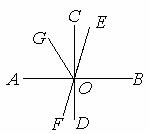
如圖,已知AB、CD、 EF相交于點O,AB⊥CD,OG平分∠AOE,∠FOD=28°,求∠COE、∠AOE、∠AOG的度數(shù).
EF相交于點O,AB⊥CD,OG平分∠AOE,∠FOD=28°,求∠COE、∠AOE、∠AOG的度數(shù).
 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
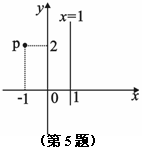
如圖,在平 面直角坐標系中,點P(-1,2)關(guān)于直線x=1的對稱點的坐標為( )
面直角坐標系中,點P(-1,2)關(guān)于直線x=1的對稱點的坐標為( )
A.(1,2) B.(2,2) C.(3,2) D.(4,2)
 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
若一個四邊形的一條對角線把四邊形分成兩個等腰三角形,我們把這條對角線叫這個四邊 形的和諧線,這個四邊形叫做和諧四邊形.在四邊形ABCD中,AB=AD=BC,∠BAD=90°,AC是四邊形ABCD的和諧線,則∠BC
形的和諧線,這個四邊形叫做和諧四邊形.在四邊形ABCD中,AB=AD=BC,∠BAD=90°,AC是四邊形ABCD的和諧線,則∠BC D=
D=
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com