【題目】正方形
、
、
、…按如圖所示的方式放置.點
、
、
、…和點
、
、
、…分別在直線
和
軸上，則點
的坐標是__________．（
為正整數）
【答案】
【解析】由圖和條件可知A1（0，1）A2（1，2）A3（3，4），B1（1，1），B2（3，2），Bn的橫坐標為An+1的橫坐標，縱坐標為An的縱坐標，又An的橫坐標數列為An=2n-1-1，所以縱坐標為（2n-1），然后就可以求出Bn的坐標為[A（n+1）的橫坐標，An的縱坐標]．
由圖和條件可知A1（0，1）A2（1，2）A3（3，4），B1（1，1），B2（3，2），
∴Bn的橫坐標為An+1的橫坐標，縱坐標為An的縱坐標，
又An的橫坐標數列為An=2n-1-1，所以縱坐標為2n-1，
∴Bn的坐標為[A（n+1）的橫坐標，An的縱坐標]=（2n-1，2n-1）．
故答案為：（2n-1，2n-1）．
科目：初中數學 來源： 題型：
【題目】如圖1，在表盤上12：00時，時針、分針都指向數字12，我們將這一位置稱為“標準位置”(圖中
)．小文同學為研究12點
分(
)時，時針與分針的指針位置，將時針記為
，分針記為
．如：12：30時，時針、分針的位置如圖2所示，試解決下列問題：
（1）分針每分鐘轉動 °；時針每分鐘轉動 °；
（2）當與在同一直線上時，求的值；
（3）當、、兩兩所夾的三個角
、
、
中有兩個角相等時，試求出所有符合條件的的值．(本小題中所有角的度數均不超過180°)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，以直線
上一點
為端點作射線
，使
，將一個直角三角形的直角頂點放在點處(注：
)
如圖①，若直角三角板
的一邊
放在射線
上，則
．
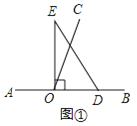
如圖②，將直角三角板繞點逆時針方向轉動到某個位置，若恰好平分
，求
的度數；
如圖③，將直角三角板繞點轉動，如果始終在
的內部，試猜想
與
有怎樣的數量關系？并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
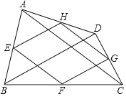
【題目】如圖，點
、
、
、
分別是四邊形
邊
、
、
、
的中點．則下列說法：①若
，則四邊形
為矩形；②若
，則四邊形為菱形；③若四邊形是平行四邊形，則
與
互相平分；④若四邊形是正方形，則與互相垂直且相等．其中正確的個數是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有兩張完全重合的矩形紙片，小亮同學將其中一張繞點A順時針旋轉90°后得到矩形AMEF（如圖1），連接BD、MF，若此時他測得BD=8cm，∠ADB=30度．請回答下列問題：（1）試探究線段BD與線段MF的關系，并簡要說明理由；
（2）小紅同學用剪刀將△BCD與△MEF剪去，與小亮同學繼續探究．他們將△ABD繞點A順時針旋轉得△AB1D1，AD1交FM于點K（如圖2），設旋轉角為β（0°＜β＜90°），當△AFK為等腰三角形時，請直接寫出旋轉角β的度數；
（3）若將△AFM沿AB方向平移得到△A2F2M2（如圖3），F2M2與AD交于點P，A2M2與BD交于點N，當NP∥AB時，求平移的距離是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AD是BC邊上的中線，E是AD的中點，過點A作BC的平行線交BE的延長線于點F，連接CF．
（1）求證：AF=DC ；
（2）若∠BAC=
，試判斷四邊形ADCF的形狀，并證明你的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某農戶承包荒山若干畝，種果樹
棵，今年水果總產量為
千克．目前有兩種銷售方式：一、此水果在市場上每千克售
元，該農戶將水果拉到市場出售平均每天出售
千克，需
人幫忙，每人每天需付工資
元，農用車運費及其他各項稅費平均每天
元．二、 直接在果園每千克售
元
．
（1）分別用
表示兩種方式出售水果的收入．
（2）若
元，
元，且兩種出售水果方式都在相同的時間內售完全部水果，請你通過計算說明選擇哪種出售方式較好?
查看答案和解析>>
科目：初中數學 來源： 題型：
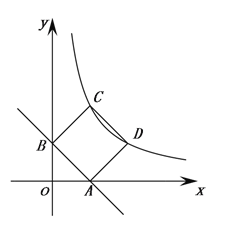
【題目】如圖：一次函數y=kx+b的圖像交x軸正半軸于點A、y軸正半軸于點B，且OA=OB=1．以線段AB為邊在第一象限作正方形ABCD，點D在反比例函數y=
圖像上．
（1）求一次函數的關系式，并判斷點C是否在反比例函數y=圖像上；
（2）在直線AB上找一點P，使PC+PD的值最小，并求出點P的坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
