
【題目】已知:如圖,在菱形![]() 中,
中,![]() ,
,![]() .點
.點![]() 為邊
為邊![]() 上的一個動點(與點
上的一個動點(與點![]() 、
、![]() 不重合),
不重合),![]() ,
,![]() 與邊
與邊![]() 相交于點
相交于點![]() ,聯結
,聯結![]() 交對角線
交對角線![]() 于點
于點![]() .設
.設![]() ,
,![]() .
.

(1)求證:![]() 是等邊三角形;
是等邊三角形;
(2)求![]() 關于
關于![]() 的函數解析式,并寫出
的函數解析式,并寫出![]() 的取值范圍;
的取值范圍;
(3)點![]() 是線段
是線段![]() 的中點,聯結
的中點,聯結![]() ,當
,當![]() 時,求
時,求![]() 的值.
的值.
【答案】(1)見解析;(2)y=![]() (0<x<2);(3)
(0<x<2);(3)![]() .
.
【解析】
(1)首先由△ABC是等邊三角形,即可得AB=AC,求得∠ACF=∠B=60°,然后利由∠BAC=∠EAF=60°,可證明∠BAE=∠CAF,從而可證得△AEB≌△AFC,即可得AE=AF,證得△AEF是等邊三角形;
(2)過點E作EH⊥AC于點H,過點F作FM⊥AC于點M,先用含x的代數式表示出HM,然后證明△EGH∽△FGM,得出![]() ,從而可用含x的代數式表示出HG,最后在Rt△EHG中,利用勾股定理可得出x,y之間的關系;
,從而可用含x的代數式表示出HG,最后在Rt△EHG中,利用勾股定理可得出x,y之間的關系;
(3)先用含x的代數式表示出CG的長,然后證明△COE∽△CGF,得出![]() ,從而可得出關于x的方程,解出x的值即可.
,從而可得出關于x的方程,解出x的值即可.
(1)證明:∵四邊形ABCD是菱形,
∴AB=BC=CD=AD,∠B=∠D=60°,
∴△ABC,△ACD都是等邊三角形,
∴AB=AC,∠B=∠ACF=60°,
∵∠BAC=∠EAF=60°,
∴∠BAE=∠CAF,
∴△BAE≌△CAF(ASA),
∴AE=AF,又∠EAF=60°,
∴△AEF為等邊三角形.
(2)解:過點E作EH⊥AC于點H,過點F作FM⊥AC于點M,
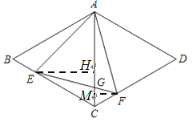
∵∠ECH=60°,∴CH=![]() ,EH=
,EH=![]() x,
x,
∵∠FCM=60°,由(1)知,CF=BE=2-x,∴CM=![]() (2-x),FM=
(2-x),FM=![]() (2-x),
(2-x),
∴HM=CH-CM=![]() -
-![]() (2-x)=x-1.
(2-x)=x-1.
∵∠EHG=∠FMG=90°,∠EGH=∠FGM,
∴△EGH∽△FGM,∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴HG=
,∴HG=![]() .
.
在Rt△EHG中,EG2=EH2+HG2,
∴y2=(![]() x)2+[
x)2+[![]() ]2,∴y2=
]2,∴y2=![]() ,∴y=
,∴y=![]() (舍去負值),
(舍去負值),
故y關于x的解析式為y=![]() (0<x<2).
(0<x<2).
(3)解:如圖,
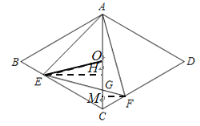
∵O為AC的中點,∴CO=![]() AC=1.
AC=1.
∵EO=EG,EH⊥OC,∴OH=GH,∠EOG=∠EGO,∴∠CGF=∠EOG.
∵∠ECG=60°,EC=x,∴CH=![]() ,∴OH=GH=OC-CH=1-
,∴OH=GH=OC-CH=1-![]() ,∴OG=2OH=2-x,
,∴OG=2OH=2-x,
∴CG=OC-OG=x-1.
∵∠CGF=∠EOC,∠ECO=∠GCF=60°,
∴△COE∽△CGF,
∴![]() ,∴
,∴![]() ,整理得x2=2,
,整理得x2=2,
∴x=![]() (舍去負值),經檢驗x是原方程的解.
(舍去負值),經檢驗x是原方程的解.
故x的值為![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 交
交![]() 軸于
軸于![]() ,
,![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() .直線
.直線![]() 經過點
經過點![]() ,
,![]() .
.
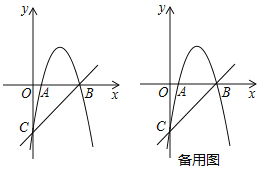
(1)求拋物線的解析式;
(2)過點![]() 的直線交直線
的直線交直線![]() 于點
于點![]() .
.
①當![]() 時,過拋物線上一動點
時,過拋物線上一動點![]() (不與點
(不與點![]() ,
,![]() 重合),作直線
重合),作直線![]() 的平行線交直線
的平行線交直線![]() 于點
于點![]() ,若以點
,若以點![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形是平行四邊形,求點
為頂點的四邊形是平行四邊形,求點![]() 的橫坐標;
的橫坐標;
②連接![]() ,當直線
,當直線![]() 與直線
與直線![]() 的夾角等于
的夾角等于![]() 的
的![]() 倍時,請直接寫出點
倍時,請直接寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點D是AB延長線上的一點,點C在⊙O上,且AC=CD,∠ACD=120°.
(1)求證:CD是⊙O的切線;
(2)若⊙O的半徑為3,求圖中陰影部分的面積.
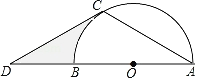
查看答案和解析>>
科目:初中數學 來源: 題型:
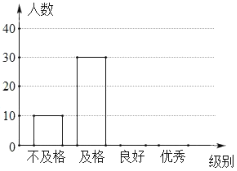
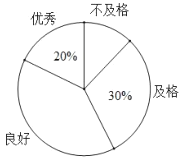
【題目】新冠肺炎疫情發(fā)生以來,專家給出了很多預防建議.為普及預防措施,某校組織了由八年級800名學生參加的“防新冠”知識競賽.李老師為了了解學生的答題情況,從中隨機抽取了部分同學的成績作為樣本,把成績按優(yōu)秀、良好、及格、不及格4個級別進行統(tǒng)計,并繪制成了如圖的條形統(tǒng)計圖和扇形統(tǒng)計圖(部分信息未給出).
請根據以上提供的信息,解答下列問題:
(1)求被抽取的部分學生的人數;
(2)請補全條形統(tǒng)計圖;
(3)求出扇形統(tǒng)計圖中表示良好級別的扇形的圓心角度數;
(4)請估計八年級的800名學生中達到良好和優(yōu)秀的總人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠BAC=90°,點O在BC上,以線段OC的長為半徑的⊙O與AB相切于點D,分別交BC、AC于點E、F,連接ED并延長,交CA的延長線于點G.
(1)求證:∠DOC=2∠G.
(2)已知⊙O的半徑為3.
①若BE=2,則DA= .
②當BE= 時,四邊形DOCF為菱形.

查看答案和解析>>
科目:初中數學 來源: 題型:
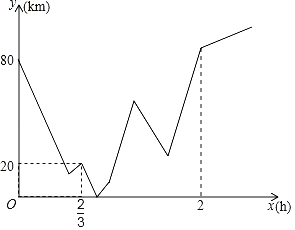
【題目】A、B兩地之間有一修理廠C,一日小海和王陸分別從A、B兩地同時出發(fā)相向而行,王陸開車,小海騎摩托.二人相遇時小海的摩托車突然出故障無法前行,王陸決定將小海和摩托車一起送回到修理廠C后再繼續(xù)按原路前行,王陸到達A地后立即返回B地,到B地后不再繼續(xù)前行,等待小海前來(裝載摩托車時間和掉頭時間忽略不計),整個行駛過程中王陸速度不變,而小海在修理廠花了十分鐘修好摩托車,為了趕時間,提速![]() 前往目的地B,小海到達B地后也結束行程,若圖象表示的是小海與王陸二人到修理廠C的距離和y(km)與小海出行時間之間x(h)的關系,則當王陸第二次與小海在行駛中相遇時,小海離目的地B還有_____km.
前往目的地B,小海到達B地后也結束行程,若圖象表示的是小海與王陸二人到修理廠C的距離和y(km)與小海出行時間之間x(h)的關系,則當王陸第二次與小海在行駛中相遇時,小海離目的地B還有_____km.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com