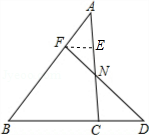
如圖,已知點F在AB上,且AF:BF=1:2,點D是BC延長線上一點,BC:CD=2:1,連接FD與AC交于點N,求FN:ND的值.

試題分析:過點F作FE∥BD,交AC于點E,求出
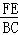
=

,得出FE=

BC,根據(jù)已知推出CD=

BC,根據(jù)平行線分線段成比例定理推出
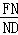
=
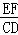
,代入化簡即可.
解:過點F作FE∥BD,交AC于點E,
∴
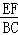
=
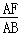
,
∵AF:BF=1:2,
∴
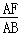
=

,
∴
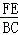
=

,
即FE=

BC,
∵BC:CD=2:1,
∴CD=

BC,
∵FE∥BD,
∴
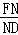
=
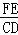
=
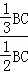
=
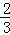
.
即FN:ND=2:3.
證法二、連接CF、AD,
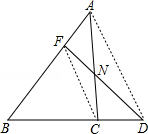
∵AF:BF=1:2,BC:CD=2:1,
∴
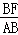
=

=
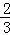
,
∵∠B=∠B,
∴△BCF∽△BDA,
∴
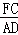
=

=
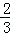
,∠BCF=∠BDA,
∴FC∥AD,
∴△CNF∽△AND,
∴
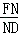
=
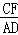
=
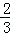
.
點評:本題考查了平行線分線段成比例定理的應(yīng)用,注意:平行線分的線段對應(yīng)成比例,此題具有一定的代表性,但是一定比較容易出錯的題目.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:初中數(shù)學(xué)
來源:不詳
題型:解答題
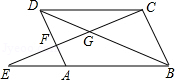
已知:?ABCD中,E是BA邊延長線上一點,CE交對角線DB于點G,交AD邊于點F.
求證:CG
2=GF•GE.
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:填空題
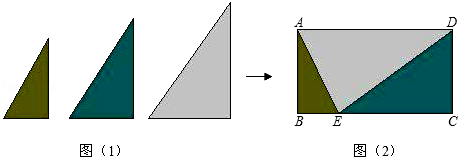
如圖(1),用形狀相同、大小不等的三塊直角三角形木板,恰好能拼成如圖(2)所示的四邊形ABCD、若AE=4,CE=3BE,那么這個四邊形的面積是
_________ .
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:填空題
在四邊形ABCD與A′B′C′D′中,∠A=∠A′,∠B=∠B′,∠C=∠C′,∠D=∠D′,且
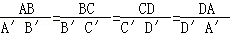
=
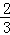
,則四邊形
ABCD ∽四邊形
A′B′C′D′ ,且四邊形ABCD與A′B′C′D′的相似比是
,四邊形ABCD與A′B′C′D′的面積比是
.
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:單選題
如圖,平行四邊形ABCD中,過點B的直線與對角線AC、邊AD分別交于點E和F.過點E作EG∥BC,交AB于G,則圖中相似三角形有( )
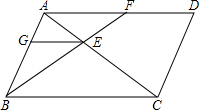
A.4對 B.5對 C.6對 D.7對
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:單選題
如圖,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于點D,若AC=2,則AD的長是( )
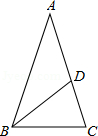
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:解答題
已知a、b、c、d四條線段依次成比例,其中a=3cm,b=(x﹣1)cm,c=5cm,d=(x+1)cm.求x的值.
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:單選題
已知
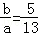
,則
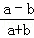
的值是( )
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:填空題
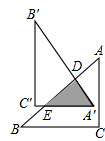
如圖,在Rt△ABC中,∠C=90°,AC=6,BC=8.把△ABC繞AB邊上的點D順時針旋轉(zhuǎn)90°得到△A′B′C′,A′C′交AB于點E.若AD=BE,則△A′DE的面積是
.
查看答案和解析>>


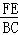 =
= ,得出FE=
,得出FE= BC,根據(jù)已知推出CD=
BC,根據(jù)已知推出CD= BC,根據(jù)平行線分線段成比例定理推出
BC,根據(jù)平行線分線段成比例定理推出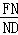 =
=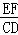 ,代入化簡即可.
,代入化簡即可.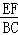 =
=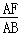 ,
,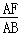 =
= ,
,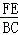 =
= ,
, BC,
BC, BC,
BC,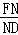 =
=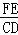 =
=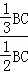 =
=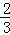 .
.
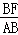 =
= =
=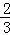 ,
,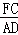 =
= =
=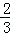 ,∠BCF=∠BDA,
,∠BCF=∠BDA,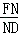 =
=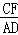 =
=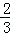 .
.


 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學(xué)教材完全解讀系列答案
小學(xué)教材完全解讀系列答案
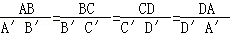 =
=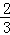 ,則四邊形 ABCD ∽四邊形 A′B′C′D′ ,且四邊形ABCD與A′B′C′D′的相似比是 ,四邊形ABCD與A′B′C′D′的面積比是 .
,則四邊形 ABCD ∽四邊形 A′B′C′D′ ,且四邊形ABCD與A′B′C′D′的相似比是 ,四邊形ABCD與A′B′C′D′的面積比是 .

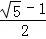
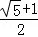
 ﹣1
﹣1 +1
+1