【題目】在平面直角坐標系中，點（a，5）關于原點對稱的點的坐標是（1，b+1），則點（a，b）在第象限．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
【題目】某班“數學興趣小組”對函數y=x2﹣2|x|的圖象和性質進行了探究，探究過程如下，請補充完整．（1）自變量x的取值范圍是全體實數，x與y的幾組對應值列表如下：
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中，m= ．
（2）根據表中數據，在如圖所示的平面直角坐標系中描點，并畫出了函數圖象的一部分，請畫出該函數圖象的另一部分．
（3）觀察函數圖象，寫出兩條函數的性質．
（4）進一步探究函數圖象發現：
①函數圖象與x軸有 個交點，所以對應的方程x2﹣2|x|=0有 個實數根；
②方程x2﹣2|x|=2有 個實數根.
③關于x的方程x2﹣2|x|=a有4個實數根時，a的取值范圍是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖（1），在矩形ABCD中，AB=4，BC=6，P是AD的中點，N是BC延長線上一點，連結PN，過點P作PN的垂線，交AB于點E，交CD的延長線于點F，連結EN，FN，設CN=x，AE=y．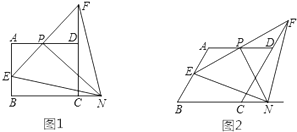
（1）求證：PE=PF；
（2）當0＜x＜ 
時，求y關于x的函數表達式；
（3）若將“矩形ABCD”變為“菱形ABCD”，如圖（2），AB=BC=4，∠B=60°，當0＜x＜3時，其它條件不變，求此時y關于x的函數表達式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】輪船沿江從A港順流行駛到B港，比從B港返回A港少用3小時，若船速為26千米/時，水速為2千米/時，求A港和B港相距多少千米．設A港和B港相距x千米．根據題意，可列出的方程是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
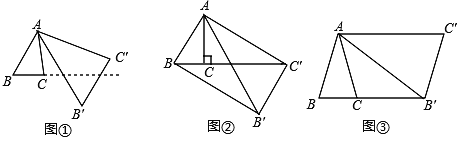
【題目】將△ABC繞點A按逆時針方向旋轉θ度，并使各邊長變為原來的n倍，得△AB′C′ ，如圖①所示，∠BAB′ ＝θ， 
，我們將這種變換記為[θ，n] ．
（1）如圖①，對△ABC作變換[60°，
]得到△AB′C′ ，則
:
= ；直線BC與直線B′C′所夾的銳角為 度；
（2）如圖②，△ABC中，∠BAC=30°，∠ACB=90°，對△ABC作變換[θ，n]得到△AB′C′，使點B、C、
在同一直線上，且四邊形ABB′C′為矩形，求θ和n的值；
（3）如圖③，△ABC中，AB=AC，∠BAC=36°，BC=1，對△ABC作變換[θ，n]得到△AB′C′，使點B、C、B′在同一直線上，且四邊形ABB′C′為平行四邊形，求θ和n的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
