
【題目】在平面直角坐標(biāo)系中,一副含![]() 和
和![]() 角的三角板
角的三角板![]() 和
和![]() 如圖擺放,邊
如圖擺放,邊![]() 與
與![]() 重合,
重合,![]() .當(dāng)點(diǎn)
.當(dāng)點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)沿
出發(fā)沿![]() 方向滑動(dòng)時(shí),點(diǎn)
方向滑動(dòng)時(shí),點(diǎn)![]() 同時(shí)從點(diǎn)
同時(shí)從點(diǎn)![]() 出發(fā)沿
出發(fā)沿![]() 軸正方向滑動(dòng).
軸正方向滑動(dòng).
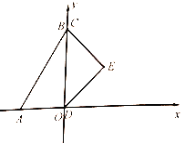
![]() 設(shè)點(diǎn)
設(shè)點(diǎn)![]() 關(guān)于
關(guān)于![]() 的函數(shù)表達(dá)式為________.
的函數(shù)表達(dá)式為________.
![]() 連接
連接![]() .當(dāng)點(diǎn)
.當(dāng)點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 滑動(dòng)到點(diǎn)
滑動(dòng)到點(diǎn)![]() 時(shí),
時(shí),![]() 的面積最大值為_______.
的面積最大值為_______.
【答案】y=x ![]()
【解析】
(1)根據(jù)題意,判定點(diǎn)E在DE所在的直線上運(yùn)動(dòng),即可得出函數(shù)表達(dá)式;
(2)首先判定點(diǎn)E的運(yùn)動(dòng)軌跡,當(dāng)E′F⊥DF時(shí),![]() 的面積最大,然后利用等腰直角三角形以及解直角三角形,即可得出E′F,進(jìn)而得出△AOE面積.
的面積最大,然后利用等腰直角三角形以及解直角三角形,即可得出E′F,進(jìn)而得出△AOE面積.
(1)由題意,得當(dāng)點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)沿
出發(fā)沿![]() 方向滑動(dòng)時(shí),點(diǎn)
方向滑動(dòng)時(shí),點(diǎn)![]() 同時(shí)從點(diǎn)
同時(shí)從點(diǎn)![]() 出發(fā)沿
出發(fā)沿![]() 軸正方向滑動(dòng)時(shí),點(diǎn)E在DE所在的直線上運(yùn)動(dòng),
軸正方向滑動(dòng)時(shí),點(diǎn)E在DE所在的直線上運(yùn)動(dòng),
∵CDE為![]() 角的三角板
角的三角板
∴![]() 關(guān)于
關(guān)于![]() 的函數(shù)表達(dá)式為
的函數(shù)表達(dá)式為![]() ;
;
(2)當(dāng)點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 滑動(dòng)到點(diǎn)
滑動(dòng)到點(diǎn)![]() 時(shí),點(diǎn)E的運(yùn)動(dòng)軌跡為E-E′-E,當(dāng)E′F⊥DF時(shí),
時(shí),點(diǎn)E的運(yùn)動(dòng)軌跡為E-E′-E,當(dāng)E′F⊥DF時(shí),![]() 的面積最大,如圖所示:
的面積最大,如圖所示:
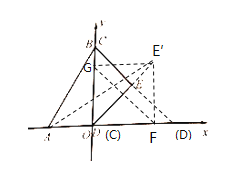
由(1)知,∠E′DF=45°
∴四邊形GOFE′為正方形
∴△COE≌△GFE′
∴OE′=OC
∵∠ABO=30°,![]()
∴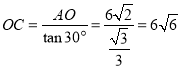
∴![]()
∴![]() 的面積為
的面積為![]()
故答案為:![]() ;
;![]() .
.


 探究與鞏固河南科學(xué)技術(shù)出版社系列答案
探究與鞏固河南科學(xué)技術(shù)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
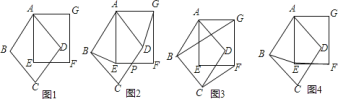
【題目】我們給定兩個(gè)全等的正方形![]() 、
、![]() ,它們共頂點(diǎn)
,它們共頂點(diǎn)![]() (如圖
(如圖![]() ),可以繞頂點(diǎn)
),可以繞頂點(diǎn)![]() 旋轉(zhuǎn),
旋轉(zhuǎn),![]() ,
,![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,以下各問(wèn)題都以此為前提.
,以下各問(wèn)題都以此為前提.
問(wèn)題要求:
![]() 連接
連接![]() 、
、![]() (如圖
(如圖![]() ),求證:
),求證:![]() ,
,![]() ;
;
![]() 連接
連接![]() 、
、![]() (如圖
(如圖![]() ),有三個(gè)結(jié)論:
),有三個(gè)結(jié)論:
①![]() ;
;
②![]() ;
;
③![]() 與
與![]() 位似.
位似.
請(qǐng)你從①,②,③三個(gè)結(jié)論中選擇一個(gè)進(jìn)行證明:
(說(shuō)明:選①做對(duì)的得![]() 分,選②做對(duì)的得
分,選②做對(duì)的得![]() 分,選③做對(duì)的得
分,選③做對(duì)的得![]() 分)
分)
![]() 連接
連接![]() 、
、![]() (如圖
(如圖![]() ),求
),求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】甲、乙兩車從A地出發(fā),勻速駛向B地.甲車以80km/h的速度行駛1h后,乙車才沿相同路線行駛.乙車先到達(dá)B地并停留1h后,再以原速按原路返回,直至與甲車相遇.在此過(guò)程中,兩車之間的距離y(km)與乙車行駛時(shí)間x(h)之間的函數(shù)關(guān)系如圖所示.下列說(shuō)法:①乙車的速度是120km/h;②m=160;③點(diǎn)H的坐標(biāo)是(7,80);④n=7.5.
其中說(shuō)法正確的是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,平面直角坐標(biāo)系中,點(diǎn)A(2,9),B(2,3),C(3,2),D(9,2)在⊙P上,Q是⊙P上的一個(gè)動(dòng)點(diǎn).
(1)在圖中標(biāo)出圓心P位置,寫出點(diǎn)P坐標(biāo);
(2)Q點(diǎn)在圓上坐標(biāo)為何值時(shí),△ABQ是直角三角形.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
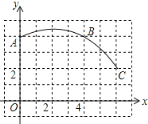
【題目】如圖,一段圓弧與長(zhǎng)度為1的正方形網(wǎng)格的交點(diǎn)是A、B、C.
(1)請(qǐng)完成以下操作:
①以點(diǎn)O為原點(diǎn),垂直和水平方向?yàn)檩S,網(wǎng)格邊長(zhǎng)為單位長(zhǎng),建立平面直角坐標(biāo)系;
②根據(jù)圖形提供的信息,標(biāo)出該圓弧所在圓的圓心D,并連接AD、CD;
(2)請(qǐng)?jiān)?/span>(1)的基礎(chǔ)上,完成下列填空:⊙D的半徑為__________;點(diǎn)(6,–2)在⊙D__________;(填“上”、“內(nèi)”、“外”)∠ADC的度數(shù)為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,已知直線![]() 交
交![]() 軸、
軸、![]() 軸分別于
軸分別于![]() 兩點(diǎn),平行于
兩點(diǎn),平行于![]() 軸的直線
軸的直線![]() 從點(diǎn)
從點(diǎn)![]() 開始以每秒
開始以每秒![]() 個(gè)單位的速度向
個(gè)單位的速度向![]() 軸的負(fù)方向運(yùn)動(dòng),直線
軸的負(fù)方向運(yùn)動(dòng),直線![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,交直線
,交直線![]() 于點(diǎn)
于點(diǎn)![]() ,設(shè)直線
,設(shè)直線![]() 的運(yùn)動(dòng)時(shí)間為
的運(yùn)動(dòng)時(shí)間為![]() 秒.
秒.

![]() 求線段
求線段![]() 的長(zhǎng).
的長(zhǎng).
![]() 若
若![]() 為直線
為直線![]() 上一動(dòng)點(diǎn),將
上一動(dòng)點(diǎn),將![]() 沿著
沿著![]() 翻折,當(dāng)點(diǎn)
翻折,當(dāng)點(diǎn)![]() 的對(duì)應(yīng)點(diǎn)
的對(duì)應(yīng)點(diǎn)![]() 落在直線
落在直線![]() 上時(shí),求直線
上時(shí),求直線![]() 的解析式.
的解析式.
![]() 若
若![]() 為
為![]() 的中點(diǎn),當(dāng)
的中點(diǎn),當(dāng)![]() 是等腰三角形時(shí),求
是等腰三角形時(shí),求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
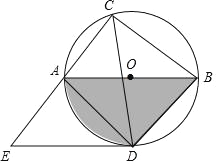
【題目】如圖,⊙O的直徑AB=12,弦AC=6,∠ACB的平分線交⊙O于D,過(guò)點(diǎn)D作DE∥AB交CA的延長(zhǎng)線于點(diǎn)E,連接AD,BD.
(1)由AB,BD,![]() 圍成的陰影部分的面積是 ;
圍成的陰影部分的面積是 ;
(2)求線段DE的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
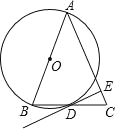
【題目】如圖,在等腰△ABC中,AB=AC,以AB為直徑作⊙O交底邊BC于D.
(1)求證:BD=CD;
(2)若AB=3,cos∠ABC=![]() ,在腰AC上取一點(diǎn)E使AE=
,在腰AC上取一點(diǎn)E使AE=![]() ,試判斷DE與⊙O的位置關(guān)系,并證明.
,試判斷DE與⊙O的位置關(guān)系,并證明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,菱形![]() 的周長(zhǎng)為
的周長(zhǎng)為![]() ,
,![]() ,垂足為
,垂足為![]() ,
,![]() ,則下列結(jié)論中正確的個(gè)數(shù)為( )
,則下列結(jié)論中正確的個(gè)數(shù)為( )
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.

A. 4個(gè) B. 3個(gè) C. 2個(gè) D. 1個(gè)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com