
【題目】如圖,在等腰△ABC中,AB=AC,以AB為直徑作⊙O交底邊BC于D.
(1)求證:BD=CD;
(2)若AB=3,cos∠ABC=![]() ,在腰AC上取一點E使AE=
,在腰AC上取一點E使AE=![]() ,試判斷DE與⊙O的位置關系,并證明.
,試判斷DE與⊙O的位置關系,并證明.
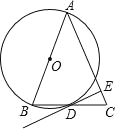
【答案】(1)證明見解析;(2)DE與⊙O相切;理由見解析;
【解析】
(1)連結AD,如圖,根據圓周角角定理,由AB為直徑得∠ADB=90°,然后根據等腰三角形的性質可得BD=CD;
(2)連結OD,如圖,在Rt△ABD中,先利用余弦定義計算出BD=![]() AB=1,則Cd=1,再利用勾股定理計算出AD=2
AB=1,則Cd=1,再利用勾股定理計算出AD=2![]() ,則有
,則有![]() ,加上∠DAE=∠CAD,于是可判斷△ADE∽△ACD,所以∠AED=∠ADC=90°,接著證明OD為△ABC的中位線得到OD∥AC,所以OD⊥DE,則根據切線的判定定理可判斷DE為⊙O的切線.
,加上∠DAE=∠CAD,于是可判斷△ADE∽△ACD,所以∠AED=∠ADC=90°,接著證明OD為△ABC的中位線得到OD∥AC,所以OD⊥DE,則根據切線的判定定理可判斷DE為⊙O的切線.
(1)證明:連結AD,如圖,
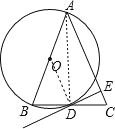
∵AB為直徑,
∴∠ADB=90°,
∴AD⊥BC,
而AB=AC,
∴BD=CD;
(2)解:DE與⊙O相切.理由如下:
連結OD,如圖,
在Rt△ABD中,∵cos∠ABD=![]() ,
,
∴BD=![]() AB=
AB=![]() ×3=1,
×3=1,
∴AD=![]() ,CD=1,
,CD=1,
∵![]() ,
,![]() ,
,
∴![]() ,
,
而∠DAE=∠CAD,
∴△ADE∽△ACD,
∴∠AED=∠ADC=90°,
∴DE⊥AC,
∵OA=OB,BD=CD,
∴OD為△ABC的中位線,
∴OD∥AC,
∴OD⊥DE,
∴DE為⊙O的切線.


 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案科目:初中數學 來源: 題型:
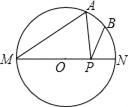
【題目】如圖,MN是⊙O的直徑,∠AMN=40°,點B為弧AN的中點,點P是直徑MN上的一個動點,如果PA+PB的最小值為![]() ,那么⊙O的直徑等于( )
,那么⊙O的直徑等于( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
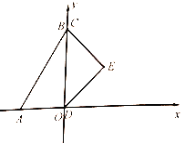
【題目】在平面直角坐標系中,一副含![]() 和
和![]() 角的三角板
角的三角板![]() 和
和![]() 如圖擺放,邊
如圖擺放,邊![]() 與
與![]() 重合,
重合,![]() .當點
.當點![]() 從點
從點![]() 出發沿
出發沿![]() 方向滑動時,點
方向滑動時,點![]() 同時從點
同時從點![]() 出發沿
出發沿![]() 軸正方向滑動.
軸正方向滑動.
![]() 設點
設點![]() 關于
關于![]() 的函數表達式為________.
的函數表達式為________.
![]() 連接
連接![]() .當點
.當點![]() 從點
從點![]() 滑動到點
滑動到點![]() 時,
時,![]() 的面積最大值為_______.
的面積最大值為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,過點![]() 的直線
的直線![]() 與直線
與直線![]() 相交于點
相交于點![]() .
.
(1)直線![]() 的關系式為 ;直線
的關系式為 ;直線![]() 的關系式為 (直接寫出答案,不必寫過程).
的關系式為 (直接寫出答案,不必寫過程).
(2)求![]() 的面積.
的面積.
(3)若有一動點![]() 沿路線
沿路線![]() 運動,當
運動,當![]() 時,求點
時,求點![]() 坐標.
坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
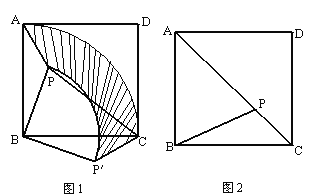
【題目】已知,點P是正方形ABCD內的一點,連PA、PB、PC.
(1)將△PAB繞點B順時針旋轉90°到△P′CB的位置(如圖1).
①設AB的長為a,PB的長為b(b<a),求△PAB旋轉到△P′CB的過程中邊PA所掃過區域(圖1中陰影部分)的面積;
②若PA=2,PB=4,∠APB=135°,求PC的長.
(2)如圖2,若PA2+PC2=2PB2,請說明點P必在對角線AC上.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某中學有一塊四邊形的空地ABCD,如圖所示,為了綠化環境,學校計劃在空地上種植草皮,經測量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面積.
(2)若每種植1平方米草皮需要200元,問總共需投入多少元?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系xOy中,橫坐標為a的點A在反比例函數y1═![]() (x>0)的圖象上,點A′與點A關于點O對稱,一次函數y2=mx+n的圖象經過點A′.
(x>0)的圖象上,點A′與點A關于點O對稱,一次函數y2=mx+n的圖象經過點A′.
(1)設a=2,點B(4,2)在函數y1、y2的圖象上.
①分別求函數y1、y2的表達式;
②直接寫出使y1>y2>0成立的x的范圍;
(2)如圖①,設函數y1、y2的圖象相交于點B,點B的橫坐標為3a,△AA'B的面積為16,求k的值;
(3)設m=![]() ,如圖②,過點A作AD⊥x軸,與函數y2的圖象相交于點D,以AD為一邊向右側作正方形ADEF,試說明函數y2的圖象與線段EF的交點P一定在函數y1的圖象上.
,如圖②,過點A作AD⊥x軸,與函數y2的圖象相交于點D,以AD為一邊向右側作正方形ADEF,試說明函數y2的圖象與線段EF的交點P一定在函數y1的圖象上.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=AC,D是線段BC的延長線上一點,以AD為一邊在AD的右側作△ADE,使AE=AD,∠DAE=∠BAC,連接CE.
(1)如圖1,點D在線段BC的延長線上移動,若∠BAC=30°,則∠DCE= .
(2)設∠BAC=α,∠DCE=β:
①如圖1,當點D在線段BC的延長線上移動時,α與β之間有什么數量關系?請說明理由;
②當點D在直線BC上(不與B、C重合)移動時,α與β之間有什么數量關系?請直接寫出你的結論.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com