
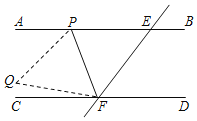
【題目】如圖,直線AB∥CD,直線l與直線AB、CD相交于點E、F,P是射線EA上的一個動點(不包括端點E),將△EFP沿PF折疊,便頂點E落在點Q處.若∠PEF=54°,且∠CFQ=![]() ∠CFP,則∠PFE的度數是_____.
∠CFP,則∠PFE的度數是_____.
 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】甲、乙兩車從A城出發勻速行駛至B城,在整個行駛過程中,甲、乙兩車離開A城的距離y(km)與行駛的時間t(h)之間的函數關系如圖所示.
(1)求乙車離開A城的距離y關于t的函數解析式;
(2)求乙車的速度.

查看答案和解析>>
科目:初中數學 來源: 題型:
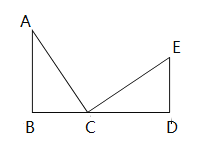
【題目】如圖,在△ABC中,∠B=90°,點B、C、D在同一直線上,△ABC≌△CDE,且∠B=∠D,∠BAC=∠DCE.
(1)試說明BD=AB+ED;
(2)若∠CED=2∠BAC,求∠CED的度數;
(3)連接AE,則△ACE是怎樣的三角形?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)用“*”表示一種新運算:對于任意正實數a,b,都有![]() .例如,
.例如,![]() ,那么15*27=__;(2)定義一種運算*,其規則為:當a≥b時,a*b=b3;當a<b時,a*b=b2.根據這個規則,方程3*x=27的解是__.
,那么15*27=__;(2)定義一種運算*,其規則為:當a≥b時,a*b=b3;當a<b時,a*b=b2.根據這個規則,方程3*x=27的解是__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P、Q是邊長為4cm的等邊△ABC邊AB、BC上的動點,點P從頂點A,點Q從頂點B同時出發,且它們的速度都為1cm/s,連接AQ、CP交于點M,則在P、Q運動的過程中,下列結論錯誤的是( )

A.BP=CM
B.△ABQ≌△CAP
C.∠CMQ的度數不變,始終等于60°
D.當第![]() 秒或第
秒或第![]() 秒時,△PBQ為直角三角形
秒時,△PBQ為直角三角形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為提供節約用水,某市按如下規定每月收取水費,若一戶居民每月用水不超過20立方米,則每立方米按3元收費;若超過20立方米,前20立方米收費標準不變,超過部分每立方米按5元收費,若某戶居民某月用水![]() 立方米.
立方米.
(1)試用含![]() (
(![]() >20)的代數式表示這戶居民該月應繳的水費.
>20)的代數式表示這戶居民該月應繳的水費.
(2)已知該市小李家1月份用水13立方米,2月份用水22立方米,3月份用水17立方米,求他家這三個月應繳納水費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD中,對角線AC=6,BD=8,M、N分別是BC、CD上的中點,P是線段BD上的一個動點,則PM+PN的最小值是( )
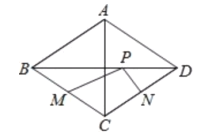
A.![]() B.3
B.3
C.![]() D.5
D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程x2﹣2(k﹣1)x+k2=0有兩個實數根x1,x2.
(1)求k的取值范圍;
(2)若|x1+x2|=x1x2﹣1,求k的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com