
【題目】重慶一中開展了“愛生活愛運動”的活動,以鼓勵學生積極參與體育鍛煉.為了解學生每周體育鍛煉時間,學校在活動之前對八年級同學進行了抽樣調査,并根據調査結果將學生每周的體育鍛煉時間分為3小時、4小時、5小時、6小時、7小時共五種情況.小明根據調查結構制作了如圖兩幅統計圖,請你結合圖中所給信息解答下列問題:
(整理數據)
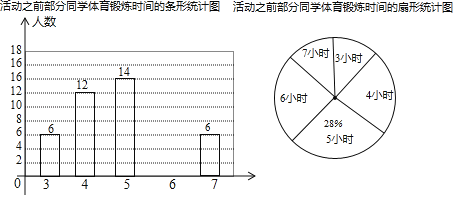
“愛生活愛運動”的活動結束之后,再次抽查這部分學生的體育鍛煉時間:
一周體育鍛煉時間(小時) | 3 | 4 | 5 | 6 | 7 |
人數 | 3 | 5 | 15 | a | 10 |
活動之后部分學生體育鍛煉時間的統計表
(分析數據)
平均數 | 中位數 | 眾數 | |
活動之前鍛煉時間(小時) | 5 | 5 | 5 |
活動之后鍛煉時間(小時) | 5.52 | b | c |
請根據調查信息
(1)補全條形統計圖,并計算a= ,b= 小時,c= 小時;
(2)小亮同學在活動之前與活動之后的這兩次調查中,體育鍛煉時間均為5小時,根據體育鍛煉時間由多到少進行排名統計,請問他在被調查同學中體育鍛煉時間排名靠前的是 (填“活動之前”或“活動之后”),理由是 ;
(3)已知八年級共2200名學生,請估算全年級學生在活動結束后,每周體育鍛煉時間至少有6小時的學生人數有多少人?
【答案】(1) 17、6、6;(2) 活動之前,活動之前小亮的體育鍛煉時間并列排名19名,而活動之后則并列排名28名;(3) 八年級2200名學生中,生在活動結束后,每周體育鍛煉時間至少有6小時的學生大約有1188人.
【解析】
(1)“體育鍛煉5小時”的有14人,占調查人數的28%,可求出調查人數,再根據活動結束后“學生體育鍛煉時間”的統計表,可求出a的值,進而再求出活動后體育鍛煉時間的中位數、眾數,確定b、c的值;
(2)得到“體育鍛煉時間5小時”在活動前、活動后的排名,即可得出結論,
(3)樣本估計總體,樣本中“每周體育鍛煉時間至少6小時”占調查人數的![]() ,估計總體2200人的
,估計總體2200人的![]() 是“每周體育鍛煉時間至少6小時”的人數.
是“每周體育鍛煉時間至少6小時”的人數.
解:(1)調查的總人數為:14÷28%=50(人),a=50﹣3﹣5﹣10﹣15=17(人),
活動結束后,再抽查,體育鍛煉時間最多的是6小時,有17人,因此眾數是6小時,
把體育鍛煉時間從小到大排列后處在第25位、26位的兩個數都是6小時,因此中位數是6,
故答案為:17、6、6;
(2)活動之前,體育鍛煉為6小時的有:50﹣6﹣12﹣14﹣6=12人,小亮5小時鍛煉時間的并列排名為:12+6+1=19名,
而活動之后,小亮5小時鍛煉時間的并列排名為:17+10+1=28名,
故答案為:活動之前,活動之前小亮的體育鍛煉時間并列排名19名,而活動之后則并列排名28名
(3)2200×![]() =1188(人),
=1188(人),
答:八年級2200名學生中,生在活動結束后,每周體育鍛煉時間至少有6小時的學生大約有1188人.


科目:初中數學 來源: 題型:
【題目】五一期間,甲、乙兩人在附近的景點游玩,甲從![]() 兩個景點中任意選擇一個游玩,乙從
兩個景點中任意選擇一個游玩,乙從![]() 三個景點中任意選擇一個游玩.
三個景點中任意選擇一個游玩.
(1)乙恰好游玩![]() 景點的概率為 .
景點的概率為 .
(2)用列表或畫樹狀圖的方法列出甲、乙恰好游玩同一景點的所有等可能的結果.并求甲、乙恰好游玩同一景點的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一張正方形紙片按如圖步驟,通過折疊得到圖④,再沿虛線剪去一個角,展開鋪平后得到圖⑤,其中![]() 是折痕.若正方形
是折痕.若正方形![]() 與五邊形
與五邊形![]() 的面積相等,則
的面積相等,則![]() 的值是( )
的值是( )
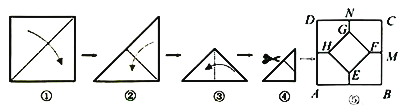
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題背景:我們學習等邊三角形時得到直角三角形的一個性質:在直角三角形中,如果一個銳角等于30°,那么它所對的直角邊等于斜邊的一半.即:如圖1,在Rt△ABC中,∠ACB=90°,∠ABC=30°,則:AC=![]() AB.
AB.

探究結論:小明同學對以上結論作了進一步研究.
(1)如圖1,連接AB邊上中線CE,由于CE=![]() AB,易得結論:①△ACE為等邊三角形;②BE與CE之間的數量關系為 .
AB,易得結論:①△ACE為等邊三角形;②BE與CE之間的數量關系為 .
(2)如圖2,點D是邊CB上任意一點,連接AD,作等邊△ADE,且點E在∠ACB的內部,連接BE.試探究線段BE與DE之間的數量關系,寫出你的猜想并加以證明.
(3)當點D為邊CB延長線上任意一點時,在(2)條件的基礎上,線段BE與DE之間存在怎樣的數量關系?請直接寫出你的結論 .
拓展應用:如圖3,在平面直角坐標系xOy中,點A的坐標為(﹣![]() ,1),點B是x軸正半軸上的一動點,以AB為邊作等邊△ABC,當C點在第一象限內,且B(2,0)時,求C點的坐標.
,1),點B是x軸正半軸上的一動點,以AB為邊作等邊△ABC,當C點在第一象限內,且B(2,0)時,求C點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=x2+(2m﹣1)x﹣2m(m>0.5)的最低點的縱坐標為﹣4.
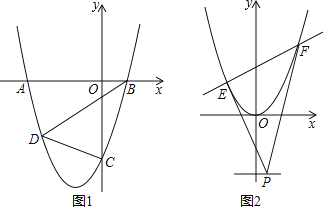
(1)求拋物線的解析式;
(2)如圖1,拋物線與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C,D為拋物線上的一點,BD平分四邊形ABCD的面積,求點D的坐標;
(3)如圖2,平移拋物線y=x2+(2m﹣1)x﹣2m,使其頂點為坐標原點,直線y=﹣2上有一動點P,過點P作兩條直線,分別與拋物線有唯一的公共點E、F(直線PE、PF不與y軸平行),求證:直線EF恒過某一定點.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在國家大數據戰略的引領下,我國在人工智能領域取得顯著成就,自主研發的人工智能“絕藝”獲得全球最前沿的人工智能賽事冠軍,這得益于所建立的大數據中心的規模和數據存儲量,它們決定著人工智能深度學習的質量和速度,其中的一個大數據中心能存儲580億本書籍,將580億用科學記數法表示應為( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD的頂點A在x軸的正半軸上,∠C=60°,頂點B,D的縱坐標相同,已知點B的橫坐標為7![]() ,若過點D的雙曲線y=
,若過點D的雙曲線y=![]() (k>0)恰好過邊AB的中點E,則k=_____.
(k>0)恰好過邊AB的中點E,則k=_____.
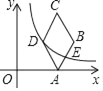
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 經過點B(3,0),C(0,-2),直線L:
經過點B(3,0),C(0,-2),直線L:![]() 交y軸于點E,且與拋物線交于A,D兩點,P為拋物線上一動點(不與A重合).
交y軸于點E,且與拋物線交于A,D兩點,P為拋物線上一動點(不與A重合).
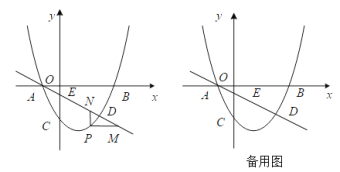
(1)求拋物線的解析式.
(2)當點P在直線L下方時,過點P作PM∥x軸交L于點M,PN∥y軸交L于點N,求PM+PN的最大值.
(3)設F為直線L上的點,以E,C,P,F為頂點的四邊形能否構成平行四邊形?若能,求出點F的坐標;若不能,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com