
【題目】如圖,拋物線![]() 經過點B(3,0),C(0,-2),直線L:
經過點B(3,0),C(0,-2),直線L:![]() 交y軸于點E,且與拋物線交于A,D兩點,P為拋物線上一動點(不與A重合).
交y軸于點E,且與拋物線交于A,D兩點,P為拋物線上一動點(不與A重合).
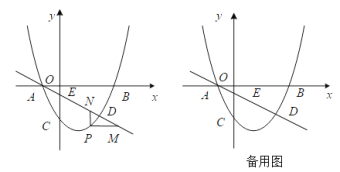
(1)求拋物線的解析式.
(2)當點P在直線L下方時,過點P作PM∥x軸交L于點M,PN∥y軸交L于點N,求PM+PN的最大值.
(3)設F為直線L上的點,以E,C,P,F為頂點的四邊形能否構成平行四邊形?若能,求出點F的坐標;若不能,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;
;
(3)能,
【解析】
(1)把B(3,0),C(0,-2)代入![]() 解方程組即可得到結論;
解方程組即可得到結論;
(2)設![]() ,
,
得到![]() ,
,![]() ,根據二次函數的性質即可得到結論;
,根據二次函數的性質即可得到結論;
(3)求得![]() ,得到
,得到![]() ,設
,設![]() ,①以CE為邊,根據CE=PF,列方程得到m=1,m=0(舍去),②以CE為對角線,連接PF交CE于G,CG=GE,PG=FG,得到
,①以CE為邊,根據CE=PF,列方程得到m=1,m=0(舍去),②以CE為對角線,連接PF交CE于G,CG=GE,PG=FG,得到![]() ,設
,設![]() ,則
,則![]() ,列方程得到此方程無實數根,于是得到結論.
,列方程得到此方程無實數根,于是得到結論.
(1)把B(3,0),C(0,-2)代入![]() 得,
得,
 ,
,
∴ ,
,
∴拋物線的解析式為:![]() ;
;
(2)設![]() ,
,
∵PM∥x軸,PN∥y軸,M,N在直線AD上,
∴![]() ,
,![]() ,
,
∴![]()
![]() ,
,
∴當![]() 時,PM+PN的最大值是
時,PM+PN的最大值是![]() ;
;
(3)能,
理由:∵![]() 交y軸于點E,
交y軸于點E,
∴![]() ,
,
∴![]() ,
,
設![]() ,
,
若以E,C,P,F為頂點的四邊形能構成平行四邊形,
①以CE為邊,∴CE∥PF,CE=PF,
∴![]() ,
,
∴![]() 或
或![]()
∴m1=1,m2=0(舍去),![]() ,
,
 ;
;
以CE為對角線,連接PF交CE于G,
∴CG=GE,PG=FG,
∴![]() ,
,
設![]() ,則
,則![]() ,
,
∴![]() ,
,
∴m=1,m=0(舍去),
∴![]() ,
,
綜上所述,
 ,
,
以E,C,P,F為頂點的四邊形能構成平行四邊形.


科目:初中數學 來源: 題型:
【題目】重慶一中開展了“愛生活愛運動”的活動,以鼓勵學生積極參與體育鍛煉.為了解學生每周體育鍛煉時間,學校在活動之前對八年級同學進行了抽樣調査,并根據調査結果將學生每周的體育鍛煉時間分為3小時、4小時、5小時、6小時、7小時共五種情況.小明根據調查結構制作了如圖兩幅統計圖,請你結合圖中所給信息解答下列問題:
(整理數據)
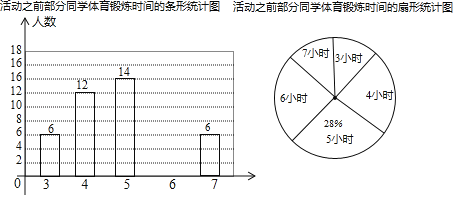
“愛生活愛運動”的活動結束之后,再次抽查這部分學生的體育鍛煉時間:
一周體育鍛煉時間(小時) | 3 | 4 | 5 | 6 | 7 |
人數 | 3 | 5 | 15 | a | 10 |
活動之后部分學生體育鍛煉時間的統計表
(分析數據)
平均數 | 中位數 | 眾數 | |
活動之前鍛煉時間(小時) | 5 | 5 | 5 |
活動之后鍛煉時間(小時) | 5.52 | b | c |
請根據調查信息
(1)補全條形統計圖,并計算a= ,b= 小時,c= 小時;
(2)小亮同學在活動之前與活動之后的這兩次調查中,體育鍛煉時間均為5小時,根據體育鍛煉時間由多到少進行排名統計,請問他在被調查同學中體育鍛煉時間排名靠前的是 (填“活動之前”或“活動之后”),理由是 ;
(3)已知八年級共2200名學生,請估算全年級學生在活動結束后,每周體育鍛煉時間至少有6小時的學生人數有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
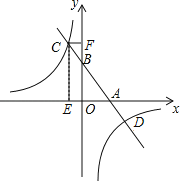
【題目】如圖,已知一次函數y=kx+b的圖象與x軸,y軸分別相交于A,B兩點,且與反比例函數y=![]() 交于點C,D.作CE⊥x軸,垂足為E,CF⊥y軸,垂足為F.點B為OF的中點,四邊形OECF的面積為16,點D的坐標為(4,﹣b).
交于點C,D.作CE⊥x軸,垂足為E,CF⊥y軸,垂足為F.點B為OF的中點,四邊形OECF的面積為16,點D的坐標為(4,﹣b).
(1)求一次函數表達式和反比例函數表達式;
(2)求出點C坐標,并根據圖象直接寫出不等式kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形![]() 的邊長為
的邊長為![]() ,點
,點![]() 分別是線段
分別是線段![]() 上的動點,連接
上的動點,連接![]() 并延長,交邊
并延長,交邊![]() 于
于![]() ,過
,過![]() 作
作![]() ,垂足為
,垂足為![]() ,交邊
,交邊![]() 于點
于點![]() .
.
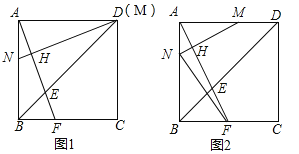
(1)如圖1,若點![]() 與點
與點![]() 重合,求證:
重合,求證:![]() ;
;
(2)如圖2,若點![]() 從點
從點![]() 出發,以
出發,以![]() 的速度沿
的速度沿![]() 向點
向點![]() 運動,同時點
運動,同時點![]() 從點
從點![]() 出發,以
出發,以![]() 的速度沿
的速度沿![]() 向點
向點![]() 運動,運動時間為
運動,運動時間為![]() .
.
①設![]() ,求
,求![]() 關于
關于![]() 的函數表達式;
的函數表達式;
②當![]() 時,連接
時,連接![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
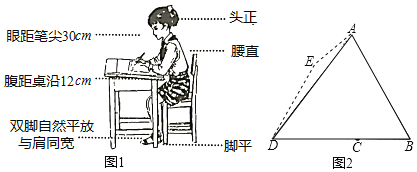
【題目】我們知道良好的坐姿有利于青少年骨骼生長,有利于身體健康,那么首先要有正確的寫字坐姿,身子上半部坐直,頭部端正、目視前方,兩手放在桌面上,兩腿平放,胸膛挺起,理想狀態下,如圖1所示,將圖1中的眼睛記為點A,腹記為點B,筆尖記為點D,且BD與桌沿的交點記為點C
(1)若∠ADB=53°,∠B=60°,求A到BD的距離及C、D兩點間的距離(結果精確到1cm).
(2)老師發現小紅同學寫字姿勢不正確,眼睛傾斜至圖2的點E,點E正好在CD的垂直平分線上,且∠BDE=60°,于是要求其糾正為正確的姿勢.求眼睛所在的位置應上升的距離.(結果精確到1cm)
參考數據:sin53°≈0.80,cos53°≈0.60,.tan53°≈1.33,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,正方形OABC的邊長為4,把它內部及邊上的橫、縱坐標均為整數的點稱為整點,點P為拋物線![]() 的頂點(m為整數),當點P在正方形OABC內部或邊上時,拋物線下方(包括邊界)的整點最少有( )
的頂點(m為整數),當點P在正方形OABC內部或邊上時,拋物線下方(包括邊界)的整點最少有( )
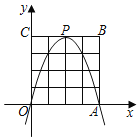
A.3個B.5個C.10個D.15個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,則下列結論:(1)4a+2b+c<0;(2)方程ax2+bx+c=0兩根都大于零;(3)y隨x的增大而增大;(4)一次函數y=x+bc的圖象一定不過第二象限.其中正確的個數是( )
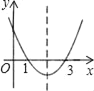
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校實施新課程改革以來,學生的學習能力有了很大提高.王老師為進一步了解本班學生自主學習、合作交流的現狀,對該班部分學生進行調查,把調查結果分成四類(A:特別好,B:好,C:一般,D:較差)后,再將調查結果繪制成兩幅不完整的統計圖(如圖1,2).請根據統計圖解答下列問題:
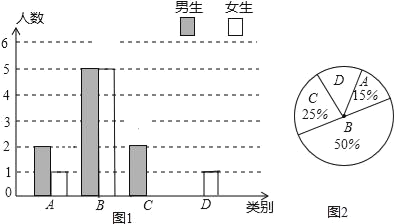
(1)本次調查中,王老師一共調查了 名學生;
(2)將條形統計圖補充完整;
(3)為了共同進步,王老師從被調查的A類和D類學生中分別選取一名學生進行“兵教兵”互助學習,請用列表或畫樹狀圖的方法求出恰好選中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
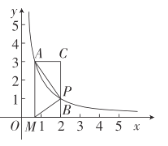
【題目】如圖,在平面直角坐標系中,點A(![]() ,3)在反比例函數C:y=
,3)在反比例函數C:y=![]() (x>0)上,點P是反比例函數C:y=
(x>0)上,點P是反比例函數C:y=![]() (x>0)上-動點,連接AP,點M在x軸上,且滿足MP⊥AP,垂足為P.
(x>0)上-動點,連接AP,點M在x軸上,且滿足MP⊥AP,垂足為P.
(1)求反比例函數的解析式;
(2)若點P(2,n),求PM所在直線的解析式;
(3)PB⊥x軸,B為垂足,CA⊥y軸,BP的延長線交AC于點C,當△AMP與△APC相似時,請寫出∠AMP與∠BMP的數量關系,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com