
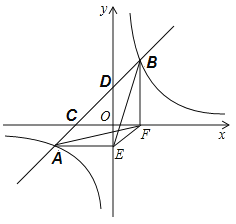
【題目】在一次數(shù)學(xué)課上,李老師出示一道開(kāi)放題,讓同學(xué)們依據(jù)已知條件寫(xiě)出正確結(jié)論,具體如下:如圖,直線(xiàn)![]() 與雙曲線(xiàn)
與雙曲線(xiàn)![]() 相交于
相交于![]() ,
,![]() 兩點(diǎn),過(guò)點(diǎn)
兩點(diǎn),過(guò)點(diǎn)![]() 和
和![]() 分別作
分別作![]() 軸和
軸和![]() 軸的垂線(xiàn),垂足分別為
軸的垂線(xiàn),垂足分別為![]() ,
,![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,直線(xiàn)
,直線(xiàn)![]() 與
與![]() 軸和
軸和![]() 軸分別交于點(diǎn)
軸分別交于點(diǎn)![]() ,
,![]() .若點(diǎn)
.若點(diǎn)![]() 坐標(biāo)
坐標(biāo)![]() ,請(qǐng)寫(xiě)出正確結(jié)論.聰明的強(qiáng)強(qiáng)很快寫(xiě)出了四個(gè)結(jié)論,其中不正確的結(jié)論是( )
,請(qǐng)寫(xiě)出正確結(jié)論.聰明的強(qiáng)強(qiáng)很快寫(xiě)出了四個(gè)結(jié)論,其中不正確的結(jié)論是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】D
【解析】
連接AO,BO,利用待定系數(shù)法求出一次函數(shù)和反比例函數(shù)解析式,再對(duì)各選項(xiàng)進(jìn)行判斷即可得出答案.
如圖,連接AO,BO,將![]() 的坐標(biāo)
的坐標(biāo)![]() 代入
代入![]() ,可得b=2,
,可得b=2,
∴直線(xiàn)解析式為![]() ,雙曲線(xiàn)解析式為
,雙曲線(xiàn)解析式為![]() ,
,
則點(diǎn)B(2,4),由反比例函數(shù)的對(duì)稱(chēng)性可知AE=BF=4,OE=OF=2,
易得OC=OD=2,則有:
A、![]() ,故正確;
,故正確;
B、![]()
故![]() ,本選項(xiàng)正確;
,本選項(xiàng)正確;
C、 易證AF=BE,則在在![]() 和
和![]() 中,
中,
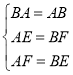
∴![]() ,本選項(xiàng)正確;
,本選項(xiàng)正確;
D、由勾股定理得![]() ,
, ![]()
![]() =1:3,本選項(xiàng)錯(cuò)誤;
=1:3,本選項(xiàng)錯(cuò)誤;
故選D.


 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】問(wèn)題探究,
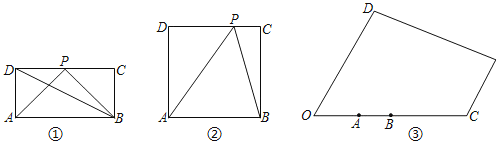
(1)如圖①,在矩形ABCD中,AB=2AD,P為CD邊上的中點(diǎn),試比較∠APB和∠ADB的大小關(guān)系,并說(shuō)明理由;
(2)如圖②,在正方形ABCD中,P為CD上任意一點(diǎn),試問(wèn)當(dāng)P點(diǎn)位于何處時(shí)∠APB最大?并說(shuō)明理由;
問(wèn)題解決
(3)某兒童游樂(lè)場(chǎng)的平面圖如圖③所示,場(chǎng)所工作人員想在OD邊上點(diǎn)P處安裝監(jiān)控裝置,用來(lái)監(jiān)控OC邊上的AB段,為了讓監(jiān)控效果最佳,必須要求∠APB最大,已知:∠DOC=60°,OA=400米,AB=200![]() 米,問(wèn)在OD邊上是否存在一點(diǎn)P,使得∠APB最大,若存在,請(qǐng)求出此時(shí)OP的長(zhǎng)和∠APB的度數(shù);若不存在,請(qǐng)說(shuō)明理由.
米,問(wèn)在OD邊上是否存在一點(diǎn)P,使得∠APB最大,若存在,請(qǐng)求出此時(shí)OP的長(zhǎng)和∠APB的度數(shù);若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】龍人文教用品商店欲購(gòu)進(jìn)![]() 、
、![]() 兩種筆記本,用160元購(gòu)進(jìn)的
兩種筆記本,用160元購(gòu)進(jìn)的![]() 種筆記本與用240元購(gòu)進(jìn)的
種筆記本與用240元購(gòu)進(jìn)的![]() 種筆記本數(shù)量相同,每本
種筆記本數(shù)量相同,每本![]() 種筆記本的進(jìn)價(jià)比每本
種筆記本的進(jìn)價(jià)比每本![]() 種筆記本的進(jìn)價(jià)貴10元.
種筆記本的進(jìn)價(jià)貴10元.
(1)求![]() 、
、![]() 兩種筆記本每本的進(jìn)價(jià)分別為多少元?
兩種筆記本每本的進(jìn)價(jià)分別為多少元?
(2)若該商店準(zhǔn)備購(gòu)進(jìn)![]() 、
、![]() 兩種筆記本共100本,且購(gòu)買(mǎi)這兩種筆記本的總價(jià)不超過(guò)2650元,則至少購(gòu)進(jìn)
兩種筆記本共100本,且購(gòu)買(mǎi)這兩種筆記本的總價(jià)不超過(guò)2650元,則至少購(gòu)進(jìn)![]() 種筆記本多少本?
種筆記本多少本?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
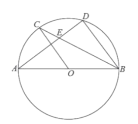
【題目】如圖,![]() 為⊙
為⊙![]() 的直徑,
的直徑,![]() ,
,![]() 為圓上的兩點(diǎn),
為圓上的兩點(diǎn),![]() ,弦
,弦![]() ,
,![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,
,
(1)求證:![]()
(2)若![]() ,
,![]() ,求⊙
,求⊙![]() 的半徑;
的半徑;
(3)在(2)的條件下,過(guò)點(diǎn)![]() 作⊙
作⊙![]() 的切線(xiàn),交
的切線(xiàn),交![]() 的延長(zhǎng)線(xiàn)于點(diǎn)
的延長(zhǎng)線(xiàn)于點(diǎn)![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 作
作![]() 交⊙
交⊙![]() 于
于![]() ,
, ![]() 兩點(diǎn)(點(diǎn)
兩點(diǎn)(點(diǎn)![]() 在線(xiàn)段
在線(xiàn)段![]() 上),求
上),求![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知AB、AC分別為⊙O的直徑和弦,D為的中點(diǎn),DE⊥AC于E,DE=6,AC=16.
(1)求證:DE是⊙O的切線(xiàn).
(2)求直徑AB的長(zhǎng).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】閱讀新知
一般地,如果一個(gè)數(shù)列從第2項(xiàng)起,每一項(xiàng)與它的前一項(xiàng)的比等于同一個(gè)非零常數(shù),這個(gè)數(shù)列就叫做等比數(shù)列.這個(gè)常數(shù)叫做等比數(shù)列的公比,公比通常用字母![]() 表示(
表示(![]() ).
).
即:在數(shù)列![]() ,
,![]() ,
,![]() ,…,
,…,![]() .(
.(![]() 為正整數(shù))中,若
為正整數(shù))中,若![]() ,
,![]() ,…,則數(shù)列
,…,則數(shù)列![]() ,
,![]() ,
,![]() ,…,
,…,![]() .(
.(![]() 為正整數(shù))叫做等比數(shù)列.其中
為正整數(shù))叫做等比數(shù)列.其中![]() 叫數(shù)列的首項(xiàng),
叫數(shù)列的首項(xiàng),![]() 叫第二項(xiàng),…,
叫第二項(xiàng),…,![]() 叫第
叫第![]() 項(xiàng),
項(xiàng),![]() 叫做數(shù)列的公比.
叫做數(shù)列的公比.
例如:數(shù)列1,2,4,8,16,…是等比數(shù)列,公比![]() .
.
計(jì)算:求等比數(shù)列1,3,![]() ,
,![]() ,…,
,…,![]() 的和.
的和.
解:令![]() ,則
,則![]() .
.
因此![]() .所以
.所以![]() .
.
即![]() .
.
學(xué)以致用
(1)選擇題:下列數(shù)列屬于等比數(shù)列的是( )
A.1,2,3,4,5 B.2,6,18,21,63
C.56,28,14,7,![]() D.-11,22,-33,44,-55
D.-11,22,-33,44,-55
(2)填空題:已知數(shù)列![]() ,
,![]() ,
,![]() ,…,
,…,![]() 是公比為4的等比數(shù)列,若它的首項(xiàng)
是公比為4的等比數(shù)列,若它的首項(xiàng)![]() ,則它的第
,則它的第![]() 項(xiàng)
項(xiàng)![]() 等于_________.
等于_________.
(3)解答題:求等比數(shù)列1,5,![]() ,
,![]() ,…前2021項(xiàng)的和.
,…前2021項(xiàng)的和.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,已知拋物線(xiàn)![]() 與直線(xiàn)
與直線(xiàn)![]() 都經(jīng)過(guò)
都經(jīng)過(guò)![]() ,
,![]() 兩點(diǎn),該拋物線(xiàn)的頂點(diǎn)為
兩點(diǎn),該拋物線(xiàn)的頂點(diǎn)為![]() .
.
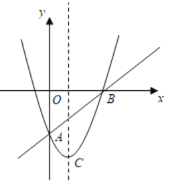
(1)求拋物線(xiàn)和直線(xiàn)![]() 的解析式;
的解析式;
(2)設(shè)點(diǎn)![]() 是直線(xiàn)
是直線(xiàn)![]() 下方拋物線(xiàn)上的一動(dòng)點(diǎn),求
下方拋物線(xiàn)上的一動(dòng)點(diǎn),求![]() 面積的最大值,并求
面積的最大值,并求![]() 面積最大時(shí),點(diǎn)
面積最大時(shí),點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】按要求作圖,不要求寫(xiě)作法,但要保留作圖痕跡.
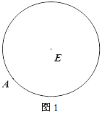
(1)如圖1,A為圓E上一點(diǎn),請(qǐng)用直尺(不帶刻度)和圓規(guī)作出圓內(nèi)接正方形;
(2)我們知道,三角形具有性質(zhì),三邊的垂直平分線(xiàn)相交于同一點(diǎn),三條角平分線(xiàn)相交于一點(diǎn),三條中線(xiàn)相交于一點(diǎn),事實(shí)上,三角形還具有性質(zhì):三條高交于同一點(diǎn),請(qǐng)運(yùn)用上述性質(zhì),只用直尺(不帶刻度)作圖:
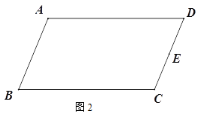
①如圖2,在□ABCD中,E為CD的中點(diǎn),作BC的中點(diǎn)F;
②圖3,在由小正方形組成的網(wǎng)格中,的頂點(diǎn)都在小正方形的頂點(diǎn)上,作△ABC的高AH
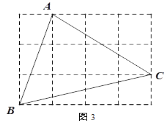
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:如圖,ABC是等腰直角三角形,∠B=90°,點(diǎn)B的坐標(biāo)為(1,2).反比例函數(shù)![]() 的圖象經(jīng)過(guò)點(diǎn)C,一次函數(shù)y=ax+b的圖象經(jīng)A,C兩點(diǎn).
的圖象經(jīng)過(guò)點(diǎn)C,一次函數(shù)y=ax+b的圖象經(jīng)A,C兩點(diǎn).
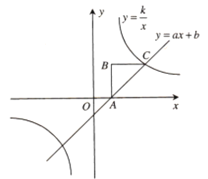
(1)求反比例函數(shù)和一次函數(shù)的關(guān)系式;
(2)直接寫(xiě)出不等式組0<ax+b≤![]() 的解集.
的解集.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com