
已知雙曲線y= (x>0),直線l1:y﹣
(x>0),直線l1:y﹣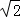 =k(x﹣
=k(x﹣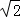 )(k<0)過定點F且與雙曲線交于A,B兩點,設A(x1,y1),B(x2,y2)(x1<x2),直線l2:y=﹣x+
)(k<0)過定點F且與雙曲線交于A,B兩點,設A(x1,y1),B(x2,y2)(x1<x2),直線l2:y=﹣x+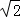 .
.
(1)若k=﹣1,求△OAB的面積S;
(2)若AB=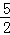
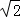 ,求k的值;
,求k的值;
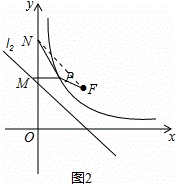
(3)設N(0,2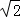 ),P在雙曲線上,M在直線l2上且PM∥x軸,求PM+PN最小值,并求PM+PN取得最小值時P的坐標.(參考公式:在平面直角坐標系中,若A(x1,y1),B(x2,y2)則A,B兩點間的距離為AB=
),P在雙曲線上,M在直線l2上且PM∥x軸,求PM+PN最小值,并求PM+PN取得最小值時P的坐標.(參考公式:在平面直角坐標系中,若A(x1,y1),B(x2,y2)則A,B兩點間的距離為AB= )
)

解:(1)當k=1時,l1:y=﹣x+2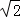 ,
,
聯立得,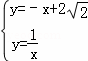 ,化簡得x2﹣2
,化簡得x2﹣2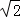 x+1=0,
x+1=0,
解得:x1=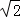 ﹣1,x2=
﹣1,x2=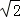 +1,
+1,
設直線l1與y軸交于點C,則C(0,2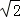 ).
).
S△OAB=S△AOC﹣S△BOC=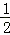 •2
•2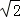 •(x2﹣x1)=2
•(x2﹣x1)=2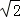 ;
;
(2)根據題意得: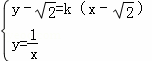 整理得:kx2+
整理得:kx2+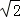 (1﹣k)x﹣1=0(k<0),
(1﹣k)x﹣1=0(k<0),
∵△=[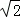 (1﹣k)]2﹣4×k×(﹣1)=2(1+k2)>0,
(1﹣k)]2﹣4×k×(﹣1)=2(1+k2)>0,
∴x1、x2 是方程的兩根,
∴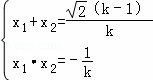 ①,
①,
∴AB=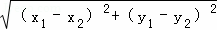 =
=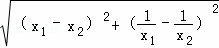 ,
,
=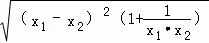 ,
,
=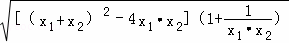 ,
,
將①代入得,AB=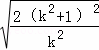 =
=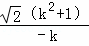 (k<0),
(k<0),
∴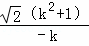 =
= ,
,
整理得:2k2+5k+2=0,
解得:k=2,或 k=﹣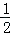 ;
;
(3)F(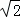 ,
,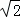 ),如圖:
),如圖:
設P(x,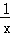 ),則M(﹣
),則M(﹣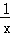 +
+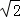 ,
,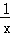 ),
),
則PM=x+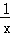 ﹣
﹣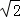 =
=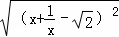 =
=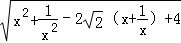 ,
,
∵PF=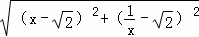 =
=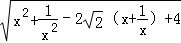 ,
,
∴PM=PF.
∴PM+PN=PF+PN≥NF=2,
當點P在NF上時等號成立,此時NF的方程為y=﹣x+2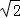 ,
,
由(1)知P(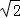 ﹣1,
﹣1,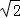 +1),
+1),
∴當P(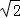 ﹣1,
﹣1,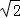 +1)時,PM+PN最小值是2.
+1)時,PM+PN最小值是2.


科目:初中數學 來源: 題型:
為推進“傳統文化進校園”活動,某校準備成立“經典誦讀”、“傳統禮儀”、“民族器樂”和“地方戲曲”等四個課外活動小組.學生報名情況如圖(每人只能選擇一個小組):
(1)報名參加課外活動小組的學生共有 100 人,將條形圖補充完整;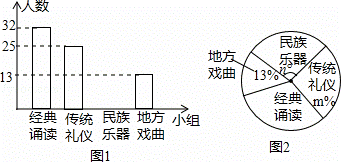
(2)扇形圖中m= ,n= ;
(3)根據報名情況,學校決定從報名“經典誦讀”小組的甲、乙、丙、丁四人中隨機安排兩人到“地方戲曲”小組,甲、乙恰好都被安排到“地方戲曲”小組的概率是多少?請用列表或畫樹狀圖的方法說明.
查看答案和解析>>
科目:初中數學 來源: 題型:
九年級(3)班共有50名同學,如圖是該班一次體育模擬測試成績的頻數分布直方圖(滿分為30分,成績均為整數).若將不低于23分的成績評為合格,則該班此次成績達到合格的同學占全班人數的百分比是 .
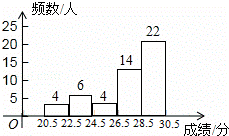
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖是一個可以自由轉動的轉盤,轉盤分為6個大小相同的扇形,指針的位置固定,轉動的轉盤停止后,其中的某個扇形會恰好停在指針所指的位置(指針指向兩個扇形的交線時,當作指向右邊的扇形),指針指向陰影區域的概率是( )

|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:初中數學 來源: 題型:
一張桌子上擺放有若干個大小、形狀完全相同的碟子,現從三個方向看,其三種視圖如圖所示,則這張桌子上碟子的總數為( )
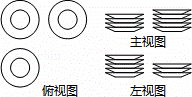
|
| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com