
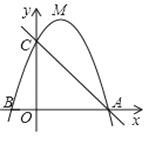
【題目】如圖,頂點為M的拋物線y=ax2+bx+3與x軸交于A(3,0),B(﹣1,0)兩點,與y軸交于點C.
(1)求拋物線的表達式;
(2)在直線AC的上方的拋物線上,有一點P(不與點M重合),使△ACP的面積等于△ACM的面積,請求出點P的坐標;
【答案】(1)![]() ;(2)P(2,3).
;(2)P(2,3).
【解析】
(1)拋物線的表達式為![]() ,即可求解;
,即可求解;
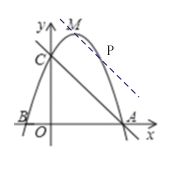
(2)過點M做直線m∥AC,直線m與拋物線的交點即為點P.
解:(1)∵y=ax2+bx+3與x軸交于A(3,0),B(﹣1,0)兩點,
設拋物線解析式為:![]()
∴![]() 解得
解得![]()
∴拋物線的表達式為:![]()
(2)由(1)得拋物線的表達式為:![]()
∴頂點M的坐標為(1,4),點C坐標為(0,3)
設直線AC的解析式為:![]() ,把A(3,0)和C(0,3)代入得
,把A(3,0)和C(0,3)代入得
![]() 解得
解得![]()
∴直線AC的解析式為:![]()
過點M做直線m∥AC,直線m與拋物線的交點即為點P,
等底同高使△ACP的面積等于△ACM的面積.
設直線m的表達式為:![]() ,
,
將M(1,4)代入得:b=5
∴直線m的表達式為:![]()
∴聯立方程組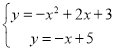 解得
解得![]()
![]()
∵點P不與點M重合
∴![]() 舍去
舍去
∴點P坐標為(2,3).
故答案為:(1)![]() ;(2)P(2,3).
;(2)P(2,3).


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:初中數學 來源: 題型:
【題目】小華和小麗設計了A、B兩種游戲:游戲A的規則是:用3張數字分別是2、3、4的撲克牌,將牌洗勻后背面朝上放置在桌面上,第一次隨機抽出一張牌記下數字后再原樣放回,洗勻后再第二次隨機抽出一張牌記下數字,若抽出的兩張牌上的數字之和為偶數,則小華獲勝;若兩數字之和為奇數,則小麗獲勝.游戲B的規則是:用4張數字分別是5、6、8、8的撲克牌,將牌洗勻后背面朝上放置在桌面上,小華先隨機抽出一張牌,抽出的牌不放回,小麗從剩下的牌中再隨機抽出一張牌,若小華抽出的牌面上的數字比小麗抽出的牌面上的數字大,則小華獲勝,否則小麗獲勝.請你幫小麗選擇其中一種游戲,使她獲勝的可能性較大,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在某體育用品商店,購買30根跳繩和60個毽子共用720元,購買10根跳繩和50個毽子共用360元.
(1)跳繩、毽子的單價各是多少元?
(2)該店在“五四”青年節期間開展促銷活動,所有商品按同樣的折數打折銷售.節日期間購買100根跳繩和100個毽子只需1800元,該店的商品按原價的幾折銷售?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學舉行鋼筆書法大賽,對各年級同學的獲獎情況進行了統計,并繪制了如下兩幅不完整的統計圖.
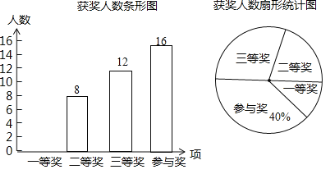
請結合圖中相關信息解答下列問題:
(1)扇形統計圖中三等獎所在扇形的圓心角的度數是______度;
(2)請將條形統計圖補全;
(3)獲得一等獎的同學中有![]() 來自七年級,有
來自七年級,有![]() 來自九年級,其他同學均來自八年級.現準備從獲得一等獎的同學中任選2人參加市級鋼筆書法大賽,請通過列表或畫樹狀圖的方法求所選出的2人中既有八年級同學又有九年級同學的概率.
來自九年級,其他同學均來自八年級.現準備從獲得一等獎的同學中任選2人參加市級鋼筆書法大賽,請通過列表或畫樹狀圖的方法求所選出的2人中既有八年級同學又有九年級同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學決定開展課后服務活動,學校就“你最想開展哪種課后服務項目”問題進行了隨機問卷調查,調查分為四個類別:![]() .舞蹈;
.舞蹈;![]() .繪畫與書法;
.繪畫與書法;![]() .球類;
.球類;![]() .不想參加.現根據調查結果整理并繪制成如下不完整的扇形統計圖和條形統計圖,請結合圖中所給信息解答下列問題:
.不想參加.現根據調查結果整理并繪制成如下不完整的扇形統計圖和條形統計圖,請結合圖中所給信息解答下列問題:
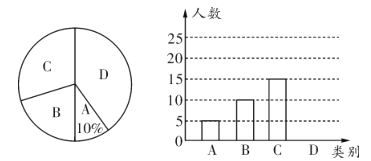
(1)這次統計共抽查了_________名學生,請補全條形統計圖;
(2)該校共有600名學生,根據以上信息,請你估計全校學生中想參加![]() 類活動的人數;
類活動的人數;
(3)若甲、乙兩名同學,各自從![]() 三個項目中隨機選一個參加,請用列表或畫樹狀圖的方法求他們選中同一項目的概率.
三個項目中隨機選一個參加,請用列表或畫樹狀圖的方法求他們選中同一項目的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC 中,∠A=30°,∠B=90°,AC=8,點 D 在邊 AB, 且 BD=![]() ,點 P 是△ABC 邊上的一個動點,若 AP=2PD 時,則 PD的長是____________.
,點 P 是△ABC 邊上的一個動點,若 AP=2PD 時,則 PD的長是____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】贛南臍橙果大形正,肉質脆嫩,風味濃甜芳香,深受大家的喜愛.某臍橙生產基地生產的禮品盒包裝的臍橙每箱的成本為30元,按定價50元出售,每天可銷售200箱.為了增加銷量,該生產基地決定采取降價措施,經市場調研,每降價1元,日銷售量可增加20箱.


(1)求出每天銷售量y(箱)與銷售單價x(元)之間的函數關系式;
(2)若該生產基地每天要實現最大銷售利潤,每箱禮品盒包裝的臍橙應定價多少元?每天可實現的最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=![]() (x-h)2+k的頂點在x軸上,其對稱軸與直線y=x交于點A(1,1),點P是拋物線上一點,以P為圓心,PA長為半徑畫圓,⊙P交x軸于B、C兩點.
(x-h)2+k的頂點在x軸上,其對稱軸與直線y=x交于點A(1,1),點P是拋物線上一點,以P為圓心,PA長為半徑畫圓,⊙P交x軸于B、C兩點.
⑴h= ,k= ;
⑵①當點P在頂點時,BC= ;
②BC的值是否隨P點橫坐標的變化而變化?如果變化,請說明理由,如果不變化,請求出這個值.
查看答案和解析>>
科目:初中數學 來源: 題型:
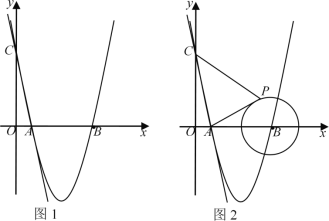
【題目】如圖1,在平面直角坐標系中,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于
軸分別交于![]() 、
、![]() 兩點,拋物線
兩點,拋物線![]() 經過
經過![]() 、
、![]() 兩點,與
兩點,與![]() 軸的另一個交點為
軸的另一個交點為![]() .
.
(1)求拋物線的解析式及![]() 點坐標;
點坐標;
(2)若點M為x軸下方拋物線上一動點,連接MA、MB、BC,當點M運動到某一位置時,四邊形AMBC面積最大,求此時點M的坐標及四邊形AMBC的面積;
(3)如圖2,若![]() 點是半徑為2的⊙
點是半徑為2的⊙![]() 上一動點,連接
上一動點,連接![]() 、
、![]() ,當點
,當點![]() 運動到某一位置時,
運動到某一位置時,![]() 的值最小為_________.(直接寫出結果)
的值最小為_________.(直接寫出結果)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com