
【題目】某中學有庫存1800套舊桌凳,修理后捐助貧困山區學校.現有甲,乙兩個木工組都想承攬這項業務.經協商后得知:甲木工組每天修理的桌凳套數是乙木工組每天修理桌凳套數的![]() ,甲木工組單獨修理這批桌凳的天數比乙木工組單獨修理這批桌凳的天數多10天,甲木工組每天的修理費用是600元,乙木工組每天的修理費用是800元.
,甲木工組單獨修理這批桌凳的天數比乙木工組單獨修理這批桌凳的天數多10天,甲木工組每天的修理費用是600元,乙木工組每天的修理費用是800元.
(1)求甲,乙兩木工組單獨修理這批桌凳的天數;
(2)現有三種修理方案供選擇:方案一,由甲木工組單獨修理這批桌凳;方案二,由乙木工組單獨修理這批桌凳;方案三,由甲,乙兩個木工組共同合作修理這批桌凳.請計算說明哪種方案學校付的修理費最少.
【答案】(1)30,20;(2)第二種方案學校付的修理費最少.
【解析】
(1)關鍵描述語為:“甲小組單獨修理這批桌凳比乙小組多用20天”;等量關系為:甲小組單獨修理這批桌凳的時間=乙小組單獨修理這批桌凳的時間+20.
(2)必須每種情況都考慮到,求出每種情況下實際花費,進行比較.
解:(1)設甲木工組單獨修理這批桌凳的天數為x天,則乙木工組單獨修理這批桌凳的天數為(x﹣10)天;
根據題意得,
![]() =
=![]() ×
×![]() ,
,
解得:x=30,
經檢驗:x=30是原方程的解.
∴x﹣10=20.
答:甲,乙兩木工組單獨修理這批桌凳的天數分別為30天,20天;
(2)方案一:甲木工組單獨修理這批桌凳的總費用:600×30=18000(元).
方案二,乙小組單獨修理,則需總費用:800×20=16000(元).
方案三,甲,乙兩個木工組共同合作修理需12(天)
總費用:(600+800)×12=16800(元)
通過比較看出:選擇第二種方案學校付的修理費最少.


科目:初中數學 來源: 題型:
【題目】如圖,△ABC是等邊三角形,D為BC邊上一個動點(D與B、C均不重合),AD=AE,∠DAE=60°,連接CE.
(1)求證:△ABD≌△ACE;
(2)求證:CE平分∠ACF;
(3)若AB=2,當四邊形ADCE的周長取最小值時,求BD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
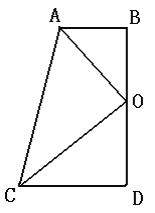
【題目】如圖,在四邊形ABDC中,∠D=∠B=90°,點O為BD的中點,且AO平分∠BAC.
(1)求證:CO平分∠ACD;
(2)求證:OA⊥OC;
(3)求證:AB+CD=AC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點A、B分別在x軸負半軸和y軸正半軸上,點C(2,-2),CA、CB分別交坐標軸于D、E,CA⊥AB,且CA=AB.
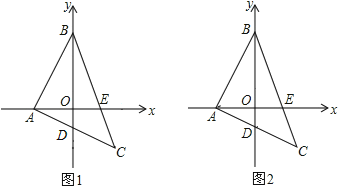
(1)求點B的坐標;
(2)如圖2,連接DE,求證:BD-AE=DE.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題:①有兩個角和第三個角的平分線對應相等的兩個三角形全等;②有兩條邊和第三條邊上的中線對應相等的兩個三角形全等;③有兩條邊和第三條邊上的高對應相等的兩個三角形全等.其中正確的是( )
A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】己知:正方形![]() .
.
![]() 如圖
如圖![]() ,點
,點![]() 、點
、點![]() 分別在邊
分別在邊![]() 和
和![]() 上,且
上,且![]() .此時,線段
.此時,線段![]() 、
、![]() 的數量關系和位置關系分別是什么?請直接寫出結論.
的數量關系和位置關系分別是什么?請直接寫出結論.
![]() 如圖
如圖![]() ,等腰直角三角形
,等腰直角三角形![]() 繞直角頂點
繞直角頂點![]() 順時針旋轉
順時針旋轉![]() ,當
,當![]() 時,連接
時,連接![]() 、
、![]() ,此時
,此時![]() 中的結論是否成立,如果成立,請證明;如果不成立,請說明理由.
中的結論是否成立,如果成立,請證明;如果不成立,請說明理由.
![]() 如圖
如圖![]() ,等腰直角三角形
,等腰直角三角形![]() 繞直角頂點
繞直角頂點![]() 順時針旋轉
順時針旋轉![]() ,當
,當![]() 時,連接
時,連接![]() 、
、![]() ,猜想溝
,猜想溝![]() 與
與![]() 滿足什么數量關系時,直線
滿足什么數量關系時,直線![]() 垂直平分
垂直平分![]() .請直接寫出結論.
.請直接寫出結論.
![]() 如圖
如圖![]() ,等腰直角三角形
,等腰直角三角形![]() 繞直角頂點
繞直角頂點![]() 順時針旋轉
順時針旋轉![]() ,當
,當![]() 時,連接
時,連接![]() 、
、![]() 、
、![]() 、
、![]() 得到四邊形
得到四邊形![]() ,則順次連接四邊形
,則順次連接四邊形![]() 各邊中點所組成的四邊形是什么特殊四邊形?請直接寫出結論.
各邊中點所組成的四邊形是什么特殊四邊形?請直接寫出結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,A(-3,0),B(0,3),DA⊥x軸,點C在OA上且∠CDB=∠ OBD,則∠CBD的度數是( )
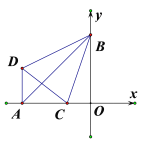
A.72°B.60°C.45°D.36°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com