
【題目】已知:如圖,四邊形ABCD四條邊上的中點分別為E、F、G、H,順次連接EF、FG、GH、HE,得到四邊形EFGH(即四邊形ABCD的中點四邊形).
(1)四邊形EFGH的形狀是_____,
證明你的結(jié)論.
(2)當(dāng)四邊形ABCD的對角線滿足_____條件時,四邊形EFGH是矩形;
(3)當(dāng)四邊形ABCD的對角線滿足_____條件時,四邊形EFGH是菱形;
(4)你學(xué)過的哪種特殊四邊形的中點四邊形是矩形?_____;
(5)你學(xué)過的哪種特殊四邊形的中點四邊形是菱形?_____;
(6)你學(xué)過的哪種特殊四邊形的中點四邊形是正方形?_____.

【答案】 平行四邊形 AC⊥BD AC=BD 菱形 矩形 正方形
【解析】試題分析:(1)連接BD,根據(jù)三角形的中位線定理得到EH∥BD,EH=![]() BD,FG∥BD,FG═
BD,FG∥BD,FG═![]() BD,推出,EH∥FG,EH=FG,根據(jù)一組對邊平行且相等的四邊形是平行四邊形得出四邊形EFGH是平行四邊形;
BD,推出,EH∥FG,EH=FG,根據(jù)一組對邊平行且相等的四邊形是平行四邊形得出四邊形EFGH是平行四邊形;
(2)根據(jù)有一個角是直角的平行四邊形是矩形,可知當(dāng)四邊形ABCD的對角線滿足AC⊥BD的條件時,四邊形EFGH是矩形;
(3)添加的條件應(yīng)為:AC=BD,把AC=BD作為已知條件,根據(jù)三角形的中位線定理可得,HG平行且等于AC的一半,EF平行且等于AC的一半,根據(jù)等量代換和平行于同一條直線的兩直線平行,得到HG和EF平行且相等,所以EFGH為平行四邊形,又EH等于BD的一半且AC=BD,所以得到所證四邊形的鄰邊EH與HG相等,所以四邊形EFGH為菱形.
(4)菱形的中點四邊形是矩形.根據(jù)三角形的中位線平行于第三邊并且等于第三邊的一半可得EH∥BD,EF∥AC,再根據(jù)矩形的每一個角都是直角可得∠1=90°,然后根據(jù)平行線的性質(zhì)求出∠3=90°,再根據(jù)垂直定義解答;
(5)菱形的中點四邊形是矩形.根據(jù)三角形的中位線平行于第三邊并且等于第三邊的一半可得EH∥BD,EF∥AC,再根據(jù)矩形的每一個角都是直角可得∠1=90°,然后根據(jù)平行線的性質(zhì)求出∠3=90°,再根據(jù)垂直定義解答;
(6)根據(jù)鄰邊相等的矩形為正方形進行解答.
試題解析:解:(1)四邊形EFGH的形狀是平行四邊形.理由如下:
如圖,連結(jié)BD.∵E、H分別是AB、AD中點,∴EH∥BD,EH=![]() BD,同理FG∥BD,FG=
BD,同理FG∥BD,FG=![]() BD,∴EH∥FG,EH=FG,∴四邊形EFGH是平行四邊形;
BD,∴EH∥FG,EH=FG,∴四邊形EFGH是平行四邊形;
(2)當(dāng)四邊形ABCD的對角線滿足互相垂直的條件時,四邊形EFGH是矩形.理由如下:
如圖,連結(jié)AC、BD.∵E、F、G、H分別為四邊形ABCD四條邊上的中點,∴EH∥BD,HG∥AC.∵AC⊥BD,∴EH⊥HG.又∵四邊形EFGH是平行四邊形,∴平行四邊形EFGH是矩形;
(3)∵E,F,G,H分別是邊AB、BC、CD、DA的中點,∴在△ADC中,HG為△ADC的中位線,所以HG∥AC且HG=![]() AC;同理EF∥AC且EF=
AC;同理EF∥AC且EF=![]() AC,同理可得EH=
AC,同理可得EH=![]() BD,則HG∥EF且HG=EF,∴四邊形EFGH為平行四邊形,又AC=BD,所以EF=EH,∴四邊形EFGH為菱形.
BD,則HG∥EF且HG=EF,∴四邊形EFGH為平行四邊形,又AC=BD,所以EF=EH,∴四邊形EFGH為菱形.
(4)菱形的中點四邊形是矩形.理由如下:
如圖,連結(jié)AC、BD.∵E、F、G、H分別為四邊形ABCD四條邊上的中點,span>∴EH∥BD,HG∥AC,FG∥BD,EH=![]() BD,FG=
BD,FG=![]() BD,∴EH∥FG,EH=FG,∴四邊形EFGH是平行四邊形.
BD,∴EH∥FG,EH=FG,∴四邊形EFGH是平行四邊形.
∵四邊形ABCD是菱形,∴AC⊥BD.∵EH∥BD,HG∥AC,∴EH⊥HG,∴平行四邊形EFGH是矩形;
(5)矩形的中點四邊形是菱形.理由如下:
理由如下:
如圖,連接AC、BD.在△ABD中,∵AH=HD,AE=EB,∴EH=![]() BD,同理FG=
BD,同理FG=![]() BD,HG=
BD,HG=![]() AC,EF=
AC,EF=![]() AC.又∵在矩形ABCD中,AC=BD,∴EH=HG=GF=FE,∴四邊形EFGH為菱形.
AC.又∵在矩形ABCD中,AC=BD,∴EH=HG=GF=FE,∴四邊形EFGH為菱形.
(6)連接AC、BD.∵E、F、G、H分別是AB、BC、CD、DA的中點,∴EF=![]() AC,GH=
AC,GH=![]() AC,EH=
AC,EH=![]() BD,GF=
BD,GF=![]() BD.∵AB=CD,∴AC=BD,∴EF=GH=EH=GF,∴四邊形EFGH菱形.∵∠HEF=90°,∴四邊形EFGH正方形.故答案為:平行四邊形;AC⊥BD;AC=BD;菱形;矩形;正方形.
BD.∵AB=CD,∴AC=BD,∴EF=GH=EH=GF,∴四邊形EFGH菱形.∵∠HEF=90°,∴四邊形EFGH正方形.故答案為:平行四邊形;AC⊥BD;AC=BD;菱形;矩形;正方形.



科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知,直線![]() 與直線
與直線![]() .
.
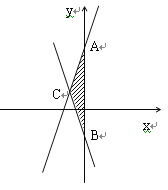
【1】(1)求兩直線與![]() 軸交點A,B的坐標;
軸交點A,B的坐標;
【2】(2)求兩直線交點C的坐標;
【3】(3)求△ABC的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,菱形![]() 的對角線
的對角線![]() 、
、![]() 相交于點
相交于點![]() ,過點
,過點![]() 作
作![]() 且
且![]() ,連接
,連接![]() 、
、![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() .
.
(1)求證:![]() ;
;
(2)若菱形![]() 的邊長為2,
的邊長為2, ![]() .求
.求![]() 的長.
的長.

【答案】(1)證明見解析(2)![]()
【解析】試題分析:(1)先求出四邊形OCED是平行四邊形,再根據(jù)菱形的對角線互相垂直求出∠COD=90°,證明OCED是矩形,可得OE=CD即可;
(2)根據(jù)菱形的性質(zhì)得出AC=AB,再根據(jù)勾股定理得出AE的長度即可.
(1)證明:在菱形ABCD中,OC=![]() AC.
AC.
∴DE=OC.
∵DE∥AC,
∴四邊形OCED是平行四邊形.
∵AC⊥BD,
∴平行四邊形OCED是矩形.
∴OE=CD.
(2)在菱形ABCD中,∠ABC=60°,
∴AC=AB=2.
∴在矩形OCED中,
CE=OD=![]() .
.
在Rt△ACE中,
AE=![]() .
.
點睛:本題考查了菱形的性質(zhì),矩形的判定與性質(zhì),勾股定理的應(yīng)用,是基礎(chǔ)題,熟記矩形的判定方法與菱形的性質(zhì)是解題的關(guān)鍵.
【題型】解答題
【結(jié)束】
25
【題目】如圖,反比例函數(shù)y=![]() 的圖象與一次函數(shù)y=kx+b的圖象交于A,B兩點,點A的坐標為(2,6),點B的坐標為(n,1).
的圖象與一次函數(shù)y=kx+b的圖象交于A,B兩點,點A的坐標為(2,6),點B的坐標為(n,1).
(1)求反比例函數(shù)與一次函數(shù)的表達式;
(2)結(jié)合圖像寫出不等式![]() 的解集;
的解集;
(3)點E為y軸上一個動點,若S△AEB=10,求點E的坐標.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某工廠計劃生產(chǎn)A,B兩種產(chǎn)品共10件,其生產(chǎn)成本和利潤如下表:
A種產(chǎn)品 | B種產(chǎn)品 | |
成本(萬元/件) | 2 | 5 |
利潤(萬元/件) | 1 | 3 |
(1)若工廠計劃獲利14萬元,問A,B兩種產(chǎn)品應(yīng)分別生產(chǎn)多少件?
(2)若工廠計劃投入資金不多于44萬元,且獲利多于14萬元,問工廠有哪幾種生產(chǎn)方案?
(3)在(2)的條件下,哪種生產(chǎn)方案獲利最大?并求出最大利潤.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,方格紙中每個小方格都是邊長為1個單位長度的正方形,△ABC的頂點和點O均在網(wǎng)格圖的格點上,將△ABC繞點O逆時針旋轉(zhuǎn)90°,得到△A1B1C1 . 
(1)請畫出△A1B1C1;
(2)以點O為圓心, ![]() 為半徑作⊙O,請判斷直線AA1與⊙O的位置關(guān)系,并說明理由.
為半徑作⊙O,請判斷直線AA1與⊙O的位置關(guān)系,并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在菱形ABCD中,AB=10,∠ABC=60°.點P從點B沿BC以每秒1個單位長的速度勻速運動,射線PF隨點P移動,始終保持與BC垂直,并交折線BA﹣AC于點E,交直線AD于點F.設(shè)點P運動時間為t秒,且點P只在BC上運動.
(1)當(dāng)t為何值時,BP=AF?
(2)設(shè)直線PF掃過菱形ABCD的面積為S,試用t的式子表示S.(寫解題過程)



查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】投擲一枚質(zhì)地均勻的正方體骰子.
(1)下列說法中正確的有 . (填序號)
①向上一面點數(shù)為1點和3點的可能性一樣大;
②投擲6次,向上一面點數(shù)為1點的一定會出現(xiàn)1次;
③連續(xù)投擲2次,向上一面的點數(shù)之和不可能等于13.
(2)如果小明連續(xù)投擲了10次,其中有3次出現(xiàn)向上一面點數(shù)為6點,這時小明說:投擲正方體骰子,向上一面點數(shù)為6點的概率是![]() . 你同意他的說法嗎?說說你的理由.
. 你同意他的說法嗎?說說你的理由.
(3)為了估計投擲正方體骰子出現(xiàn)6點朝上的概率,小亮采用轉(zhuǎn)盤來代替骰子做實驗.下圖是一個可以自由轉(zhuǎn)動的轉(zhuǎn)盤,請你將轉(zhuǎn)盤分為2個扇形區(qū)域,分別涂上紅、白兩種顏色,使得轉(zhuǎn)動轉(zhuǎn)盤,當(dāng)轉(zhuǎn)盤停止轉(zhuǎn)動后,指針落在紅色區(qū)域的概率與投擲正方體骰子出現(xiàn)6點朝上的概率相同.(友情提醒:在轉(zhuǎn)盤上用文字注明顏色和扇形圓心角的度數(shù).)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com