
【題目】如圖,在平面直角坐標系中,O是坐標原點,二次函數y=x2+c的圖象拋物線交x軸于點A,B(點A在點B的左側),與y軸交于點C(0,﹣3).
(1)求∠ABC的度數;
(2)若點D是第四象限內拋物線上一點,△ADC的面積為 ![]() ,求點D的坐標;
,求點D的坐標;
(3)若將△OBC繞平面內某一點順時針旋轉60°得到△O′B′C′,點O′,B′均落在此拋物線上,求此時O′的坐標.
【答案】
(1)解:由題意與y軸交于點C(0,﹣3),
∴得解析式為y=x2﹣3,
令y=0,x=± ![]() ,
,
∴B( ![]() ,0),A(﹣
,0),A(﹣ ![]() ,0),
,0),
∴OA= ![]() ,OC=3,AC=2
,OC=3,AC=2 ![]() ,
,
∴∠OCA=30°,
∴∠ABC=60°;
(2)解:由(1)得:OA= ![]() ,OC=3,
,OC=3,
∴S△OAC= ![]() ×3×
×3× ![]() =
= ![]() ,
,
過原點與AC平行的直線y=﹣ ![]() ,
,
直線與拋物線的交點即為點D,
聯立: ![]() ,
,
解得x1= ![]() ,x2=
,x2= ![]() (舍去),
(舍去),
∴D ( ![]() ,
, ![]() ).
).
(3)解:設點O′(m,m2﹣3),
∵順時針旋轉60°,
則點B′(m+ ![]() ,m2﹣
,m2﹣ ![]() ),
),
∴(m+ ![]() )﹣3=m2﹣
)﹣3=m2﹣ ![]() ,
,
∴m=﹣ ![]() ,
,
∴O′(﹣ ![]() ,﹣
,﹣ ![]() ).
).
【解析】(1)通過待定系數法求出函數解析式,可以求出相應的線段的長度,觀察AC=2OA,進而求出∠ABC的度數
(2)通過觀察S△ADC=S△OAC,可以判斷直線OD∥AC,求出直線與拋物線的交點即為D
(3)利用點O'B'都在拋物線上,設出點O'的坐標,通過旋轉得B’的坐標,將B’帶入拋物線解析式即可求出。
【考點精析】認真審題,首先需要了解二次函數的圖象(二次函數圖像關鍵點:1、開口方向2、對稱軸 3、頂點 4、與x軸交點 5、與y軸交點),還要掌握二次函數的性質(增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小)的相關知識才是答題的關鍵.


科目:初中數學 來源: 題型:
【題目】周末,小明坐公交車到濱海公園游玩,他從家出發0.8小時后達到中心書城,逗留一段時間后繼續坐公交車到濱海公園,小明離家一段時間后,爸爸駕車沿相同的路線前往海濱公園. 如圖是他們離家路程s(km)與小明離家時間t(h)的關系圖,請根據圖回答下列問題:
(1)圖中自變量是____,因變量是______;
(2)小明家到濱海公園的路程為____ km,小明在中心書城逗留的時間為____ h;
(3)小明出發______小時后爸爸駕車出發;
(4)圖中A點表示___________________________________;
(5)小明從中心書城到濱海公園的平均速度為______km/h,小明爸爸駕車的平均速度為______km/h;(補充;爸爸駕車經過______追上小明);
(6)小明從家到中心書城時,他離家路程s與坐車時間t之間的關系式為________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知數軸上的A、B、C、D四點所表示的數分別是a、b、c、d,且(a+16)2+(d+12)2=﹣|b﹣8|﹣|c﹣10|.
(1)求a、b、c、d的值;
(2)點A,B沿數軸同時出發相向勻速運動,4秒后兩點相遇,點B的速度為每秒2個單位長度,求點A的運動速度;
(3)A,B兩點以(2)中的速度從起始位置同時出發,向數軸正方向運動,與此同時,C點以每秒1個單位長度的速度向數軸正方向開始運動,若t秒時有2AB=CD,求t的值;
(4)A,B兩點以(2)中的速度從起始位置同時出發,相向而行當A點運動到C點時,迅速以原來速度的2倍返回,到達出發點后,保持改變后的速度又折返向C點運動;當B點運動到A點的起始位置后停止運動.當B點停止運動時,A點也停止運動.求在此過程中,A,B兩點同時到達的點在數軸上對應的數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司銷售一種進價為20 (元/個)的計算器,其銷售量y (萬個)與銷售價格x (元/個)之間為一次函數關系,其變化如下表:
價格x (元/個) | … | 30 | 50 | … |
銷售量y (萬個) | … | 5 | 3 | … |
同時,銷售過程中的其他開支(不含進價)總計40萬元.若該公司要獲得40萬元的凈利潤,且盡可能讓顧客得到實惠,那么銷售價格應定為多少?
(注:凈利潤=總銷售額﹣總進價﹣其他開支)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】
(本小題滿分8分)某學校組織八年級學生參加社會實踐活動,若單獨租用35座客車若干輛,則剛好坐滿;若單獨租用55座客車,則可以少租一輛,且余45個空座位.
(1)求該校八年級學生參加社會實踐活動的人數;
(2)已知35座客車的租金為每輛320元,55座客車的租金為每輛400元.根據租車資金不超過1500元的預算,學校決定同時租用這兩種客車共4輛(可以坐不滿).請你計算本次社會實踐活動所需車輛的租金.
查看答案和解析>>
科目:初中數學 來源: 題型:
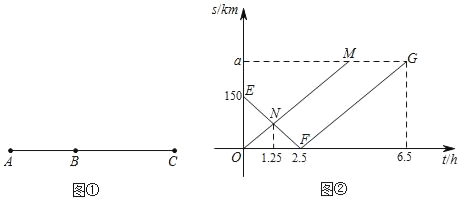
【題目】如圖①,A、B、C三地依次在一直線上,兩輛汽車甲、乙分別從A、B兩地同時出發駛向C地,如圖②,是兩輛汽車行駛過程中到C地的距離s(km)與行駛時間t(h)的關系圖象,其中折線段EF﹣FG是甲車的圖象,線段OM是乙車的圖象.
(1)圖②中,a的值為 ;點M的坐標為 ;
(2)當甲車在乙車與B地的中點位置時,求行駛的時間t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,將兩塊三角板的直角頂點重合.

(1)寫出以C為頂點的相等的角;
(2)若∠ACB=150°,請直接寫出∠DCE的度數;
(3)寫出∠ACB與∠DCE之間所具有的數量關系;
(4)當三角板ACD繞點C旋轉時,你所寫出的(3)中的關系是否變化?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面的文字,解答問題.
大家知道![]() 是無理數,而無理數是無限不循環小數,因此
是無理數,而無理數是無限不循環小數,因此![]() 的小數部分我們不可能全部地寫出來,于是小明用
的小數部分我們不可能全部地寫出來,于是小明用![]() 來表示
來表示![]() 的小數部分,你同意小明的表示方法嗎?
的小數部分,你同意小明的表示方法嗎?
事實上,小明的表示方法是有道理,因為![]() 的整數部分是1,將這個數減去其整數部分,差就是小數部分.
的整數部分是1,將這個數減去其整數部分,差就是小數部分.
請解答:(1)若![]() 的整數部分為
的整數部分為![]() ,小數部分為
,小數部分為![]() ,求
,求![]() 的值.
的值.
(2)已知:![]() ,其中
,其中![]() 是整數,且
是整數,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com