
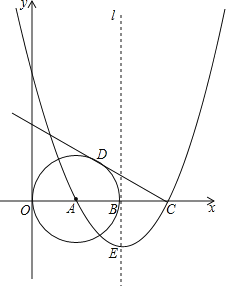
【題目】如圖,已知點A(2,0),以A為圓心作⊙A與y軸切于原點,與x軸的另一個交點為B,過B作⊙A的切線l.
(1)以直線l為對稱軸的拋物線過點A,拋物線與x軸的另一個交點為點C,拋物線的頂點為點E,如果CO=2BE,求此拋物線的解析式;
(2)過點C作⊙A的切線CD,D為切點,求此切線長;
(3)點F是切線CD上的一個動點,當△BFC與△CAD相似時,求出BF的長.
【答案】(1)y=![]() (x-2)(x-6);(2)CD=2
(x-2)(x-6);(2)CD=2![]() ;(3)BF的長為
;(3)BF的長為![]() 或
或![]() .
.
【解析】
(1)由題意可知拋物線的對稱軸為x=4,然后設出拋物線的兩點式,然后將點E的坐標代入求解即可;
(2)由于AD是⊙A的切線,連接AD,那么根據切線的性質知AD⊥CD,在Rt△ACD中,可利用勾股定理求得切線CD的長度;
(3)若△BFC與△CAD相似,則有兩種情況需要考慮:①△FBC∽△ADC,②△BFC∽△CAD,根據不同的相似三角形所得不同的比例線段即可求得CF的長.
(1)∵A(2,0),⊙A與y軸切于原點,
∴⊙A的半徑為2.
∴點B的坐標為為(4,0).
∵點A、C關于x=4對稱,
∴C(6,0).
又CO=2BE,
∴E(4,-3)
設拋物線的解析式為y=a(x-2)(x-6),(a≠0);
∵拋物線經過點E(4,-3)
∴-3=a(4-2)(4-6),
解得:a=![]() .
.
∴拋物線的解析式為y=![]() (x-2)(x-6);
(x-2)(x-6);
(2)如圖1所示:連接AD,
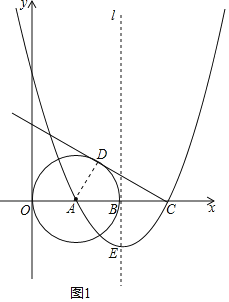
∵AD是⊙A的切線,
∴∠ADC=90°,AD=2,
由(1)知,C(6,0).
∵A(2,0),
∴AC=4,
在Rt△ACD中,CD2=AC2-AD2=42-22=12,
∴CD=2![]() .
.
(3)如圖2所示:當FB⊥AD時,連結AD.
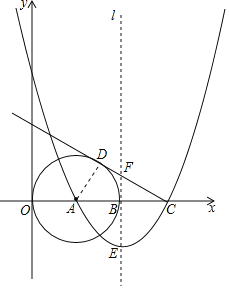
∵∠FBC=∠ADC=90°,∠FCB=∠ACD,
∴△FBC∽△ADC,
∴![]() =
=![]() ,即
,即![]() =
=![]() .
.
解得:CF=![]() .
.
如圖3所示:當BF⊥CD時,連結AD、過點B作BF⊥CD,垂足為F.
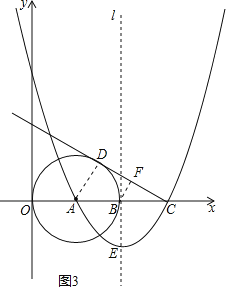
∵AD⊥CD,
∴BF∥AD,
∴△BFC∽△ADC,
∴![]() =
=![]() ,即
,即![]() =
=![]() .
.
∴CF=![]() .
.
綜上所述,BF的長為![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】小明在學習二次根式后,發現一些含根號的式子可以寫成另一個式子的平方,如:3+2![]() ,善于思考的小明進行了以下探索:
,善于思考的小明進行了以下探索:
設a+b![]() (其中a、b、m、n均為整數),
(其中a、b、m、n均為整數),
則有:a+b![]() ,∴a=m2+2n2,b=2mn,這樣小明就找到了一種把類似a+b
,∴a=m2+2n2,b=2mn,這樣小明就找到了一種把類似a+b![]() 的式子化為平方式的方法.
的式子化為平方式的方法.
請你仿照小明的方法探索并解決下列問題:
(1)當a、b、m、n均為正整數時,若a+b![]() ,用含m、n的式子分別表示a、b得:a= ,b= ;
,用含m、n的式子分別表示a、b得:a= ,b= ;
(2)利用所探索的結論,用完全平方式表示出:7+4![]() = .
= .
(3)請化簡:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,G是CD的中點,E是邊AD上的動點,EG的延長線與BC的延長線交于點F,連結CE,DF.
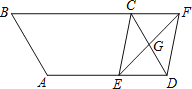
(1)求證:四邊形CEDF為平行四邊形;
(2)若AB=6cm,BC=10cm,∠B=60°,
①當AE= cm時,四邊形CEDF是矩形;
②當AE= cm時,四邊形CEDF是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一不透明的布袋里,裝有紅、黃、藍三種顏色的小球(除顏色外其余都相同),其中有紅球2個,藍球1個,黃球若干個,現從中任意摸出一個球是紅球的概率為![]() .
.
(1)求口袋中黃球的個數;
(2)甲同學先隨機摸出一個小球(不放回),再隨機摸出一個小球,請用“樹狀圖法”或“列表法”,
求兩次摸 出都是紅球的概率;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,為測量某建筑物AB的高度,在離該建筑物底部20m的點C處,目測建筑物頂端A處,視線與水平線夾角∠ADE為38.5°,目高CD為1.6m.求建筑物AB的高度.(結果精確到1m)(參考數據:sin38.5°=0.623,cos38.5°=0.783,tan38.5°=0.795)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2-4x+c,函數值y與自變量x之間的部分對應值如表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 15 | m | n | 0 | k | … |
(1)求這個二次函數的關系式.
(2)直接寫出m、n、k之間的大小關系.(用“>”連接)
(3)若點P在這個二次函數的圖象上,且點P到x軸的距離為1,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,點O是坐標原點,四邊形ABCO是菱形,點A的坐標為(﹣3,4),點C在x軸的正半軸上,直線AC交y軸于點M,AB邊交y軸于點H,連接BM.
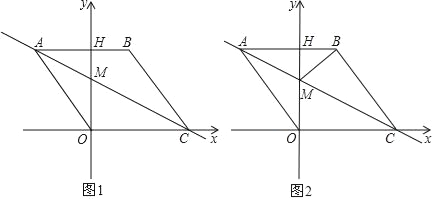
(1)菱形ABCO的邊長
(2)求直線AC的解析式;
(3)動點P從點A出發,沿折線ABC方向以2個單位/秒的速度向終點C勻速運動,設△PMB的面積為S(S≠0),點P的運動時間為t秒,
①當0<t<![]() 時,求S與t之間的函數關系式;
時,求S與t之間的函數關系式;
②在點P運動過程中,當S=3,請直接寫出t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店計劃購進甲、乙兩種商品,乙種商品的進價是甲種商品進價的九折,用3600元購買乙種商品要比購買甲種商品多買10件.
(1)求甲、乙兩種商品的進價各是多少元?
(2)該商店計劃購進甲、乙兩種商品共80件,且乙種商品的數量不低于甲種商品數量的3倍.甲種商品的售價定為每件80元,乙種商品的售價定為每件70元,若甲、乙兩種商品都能賣完,求該商店能獲得的最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com