
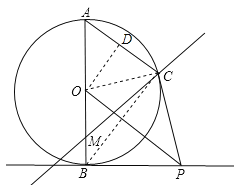
【題目】已知AB是⊙O的直徑,PB是⊙O的切線,C是⊙O上的點,AC∥OP,M是直徑AB上的動點,A與直線CM上的點連線距離的最小值為d,B與直線CM上的點連線距離的最小值為f.
(1)求證:PC是⊙O的切線;
(2)設OP=![]() AC,求∠CPO的正弦值;
AC,求∠CPO的正弦值;
(3)設AC=9,AB=15,求d+f的取值范圍.

【答案】(1)證明見解析;(2)![]() ;(3)9≤d+f≤15.
;(3)9≤d+f≤15.
【解析】試題分析:(1)連接OC,根據等腰三角形的性質得到∠A=∠OCA,由平行線的性質得到∠A=∠BOP,∠ACO=∠COP,等量代換得到∠COP=∠BOP,由切線的性質得到∠OBP=90°,根據全等三角形的性質即可得到結論;
(2)過O作OD⊥AC于D,根據相似三角形的性質得到CDOP=OC2,根據已知條件得到![]() =
=![]() ,由三角函數的定義即可得到結論;
,由三角函數的定義即可得到結論;
(3)連接BC,根據勾股定理得到BC的值,當M與A重合時,得到d+f=12,當M與B重合時,得到d+f=9,于是得到結論.
試題解析:解:(1)連接OC,∵OA=OC,∴∠A=∠OCA,∵AC∥OP,∴∠A=∠BOP,∠ACO=∠COP,∴∠COP=∠BOP,∵PB是⊙O的切線,AB是⊙O的直徑,∴∠OBP=90°,在△POC與△POB中,∵OC=OB,∠COP=∠BOP,OP=OP,∴△COP≌△BOP,∴∠OCP=∠OBP=90°,∴PC是⊙O的切線;
(2)過O作OD⊥AC于D,∴∠ODC=∠OCP=90°,CD=![]() AC,∵∠DCO=∠COP,∴△ODC∽△PCO,∴
AC,∵∠DCO=∠COP,∴△ODC∽△PCO,∴![]() ,∴CDOP=OC2,∵OP=
,∴CDOP=OC2,∵OP=![]() AC,∴AC=
AC,∴AC=![]() OP,∴CD=
OP,∴CD=![]() OP,∴
OP,∴![]() OPOP=OC2,∴
OPOP=OC2,∴![]() =
=![]() ,∴sin∠CPO=
,∴sin∠CPO=![]() =
=![]() ;
;
(3)連接BC,∵AB是⊙O的直徑,∴AC⊥BC,∵AC=9,AB=15,∴BC=![]() =12,當M與A重合時,d=0,f=AB=15,∴d+f=15,當M與B重合時,d=9,f=0,∴d+f=9,∴d+f的取值范圍是:9≤d+f≤15.
=12,當M與A重合時,d=0,f=AB=15,∴d+f=15,當M與B重合時,d=9,f=0,∴d+f=9,∴d+f的取值范圍是:9≤d+f≤15.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】調查顯示:手機每平方厘米就駐扎了120000個細菌,按照這樣的推算,整部手機起碼有上百萬個細菌.“手機控”的同學們,你可知道這個可怕的事實哦!請將120000用科學記數法表示為____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
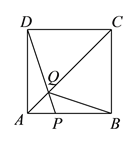
【題目】如圖,在邊長為![]() 的正方形
的正方形![]() 中,點
中,點![]() 在
在![]() 上從
上從![]() 向
向![]() 運動,連接
運動,連接![]() 交
交![]() 于點
于點![]() .
.
(![]() )試證明:無論點
)試證明:無論點![]() 運動到
運動到![]() 上何處時,都有
上何處時,都有![]() ≌
≌![]() .
.
(![]() )若點
)若點![]() 從點
從點![]() 運動到點
運動到點![]() ,再繼續在
,再繼續在![]() 上運動到點
上運動到點![]() ,在整個運動過程中,點
,在整個運動過程中,點![]() 以每秒
以每秒![]() 單位長度的速度勻速運動,當
單位長度的速度勻速運動,當![]() 恰為等腰三角形,求點
恰為等腰三角形,求點![]() 運動的時間.
運動的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
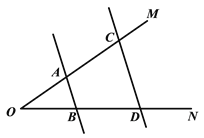
【題目】問題情境:如圖,![]() ∥
∥![]() ,
,![]() ,
,![]() ,求
,求![]() 的度數.
的度數.
小明的思路是過點![]() 作
作![]() ∥
∥![]() ,通過平行線的性質來求
,通過平行線的性質來求![]() .
.

(1)按照小明的思路,求![]() 的度數;
的度數;
(2)問題遷移:如圖,![]() ∥
∥![]() ,點
,點![]() 在射線
在射線![]() 上運動,記
上運動,記![]() ,
,![]() ,當點
,當點![]() 在
在![]() 、
、![]() 兩點之間運動時,問
兩點之間運動時,問![]() 與
與![]() 、
、![]() 之間有何數量關系?請說明理由;
之間有何數量關系?請說明理由;

(3)在(2)的條件下,如果點![]() 不在
不在![]() 、
、![]() 兩點之間運動時(點
兩點之間運動時(點![]() 與點
與點![]() 、
、![]() 、
、![]() 三點不重合),請直接寫出
三點不重合),請直接寫出![]() 與
與![]() 、
、![]() 之間的數量關系.
之間的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
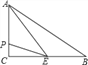
【題目】如圖,在△ABC中,∠C=90°,BC=8cm,AC=6cm,點E是BC的中點,動點P從A點出發,先以每秒2cm的速度沿A→C運動,然后以1cm/s的速度沿C→B運動.若設點P運動的時間是t秒,那么當t=_____________,△APE的面積等于6.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設![]() ,
, ![]() ,……,
,……, ![]() ,(n為正整數)
,(n為正整數)
(1)試說明![]() 是8的倍數;
是8的倍數;
(2)若△ABC的三條邊長分別為![]() 、
、![]() 、
、![]() (
(![]() 為正整數)
為正整數)
①求![]() 的取值范圍.
的取值范圍.
②是否存在這樣的![]() ,使得△ABC的周長為一個完全平方數,若存在,試舉出一例,若不存在,說明理由.
,使得△ABC的周長為一個完全平方數,若存在,試舉出一例,若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在平面直角坐標系中,二次函數y=﹣![]() x2+bx+c的圖象與坐標軸交于A,B,C三點,其中點A的坐標為(﹣3,0),點B的坐標為(4,0),連接AC,BC.動點P從點A出發,在線段AC上以每秒1個單位長度的速度向點C作勻速運動;同時,動點Q從點O出發,在線段OB上以每秒1個單位長度的速度向點B作勻速運動,當其中一點到達終點時,另一點隨之停止運動,設運動時間為t秒.連接PQ.
x2+bx+c的圖象與坐標軸交于A,B,C三點,其中點A的坐標為(﹣3,0),點B的坐標為(4,0),連接AC,BC.動點P從點A出發,在線段AC上以每秒1個單位長度的速度向點C作勻速運動;同時,動點Q從點O出發,在線段OB上以每秒1個單位長度的速度向點B作勻速運動,當其中一點到達終點時,另一點隨之停止運動,設運動時間為t秒.連接PQ.
(1)填空:b= ,c= ;
(2)在點P,Q運動過程中,△APQ可能是直角三角形嗎?請說明理由;
(3)在x軸下方,該二次函數的圖象上是否存在點M,使△PQM是以點P為直角頂點的等腰直角三角形?若存在,請求出運動時間t;若不存在,請說明理由;
(4)如圖②,點N的坐標為(﹣![]() ,0),線段PQ的中點為H,連接NH,當點Q關于直線NH的對稱點Q′恰好落在線段BC上時,請直接寫出點Q′的坐標.
,0),線段PQ的中點為H,連接NH,當點Q關于直線NH的對稱點Q′恰好落在線段BC上時,請直接寫出點Q′的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為驗證“擲一個質地均勻的骰子,向上的點數為偶數的概率是0.5”,下列模擬實驗中,不科學的是( )
A. 袋中裝有1個紅球一個綠球,它們除顏色外都相同,計算隨機摸出紅球的概率
B. 用計算器隨機地取不大于10的正整數,計算取得奇數的概率
C. 隨機擲一枚質地均勻的硬幣,計算正面朝上的概率
D. 如圖,將一個可以自由旋轉的轉盤分成甲、乙、丙3個相同的扇形,轉動轉盤任其自由停止,計算指針指向甲的概率
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com