
【題目】八年級(1)班研究性學習小組為研究全校同學課外閱讀情況,在全校隨機邀請了部分同學參與問卷調查,統計同學們一個月閱讀課外書的數量,并繪制了如下的統計圖1和圖2,請根據圖中相關信息,解決下列問題:

(Ⅰ)圖1中![]() 的值為____________,共有____________名同學參與問卷調查;
的值為____________,共有____________名同學參與問卷調查;
(Ⅱ)求統計的這組數據的平均數、眾數和中位數;
(Ⅲ)全校共有學生1500人,根據樣本數據,估計該校學生一個月閱讀2本課外書的人數約為多少?
【答案】(Ⅰ)41,100;(Ⅱ)平均數是2.54, 眾數為2,中位數為2;(Ⅲ)估計這1500名學生一個月閱讀2本課外書的人數約為:![]()
【解析】
(1)用1減去1本,3本,4本所占的比例減去即可;用閱讀一本書的人數除以它占的比例即可求出總數.
(2)平均數=![]() ,閱讀課外書的本書的人數的本書即為眾數,將涉及到的本書從小到大排列最中間的就是中位數;
,閱讀課外書的本書的人數的本書即為眾數,將涉及到的本書從小到大排列最中間的就是中位數;
(3)用總人數乘以樣本中“閱讀2本課外書”人數所占百分比可得 .
(Ⅰ)∵m%=1-15%-10%-34%=41%,
∴m=41;
10÷10%=100,
∴總人數是100人;
(Ⅱ)∵![]() ,
,
∴這組數據的平均數是2.54.
∵在這組數據中,2出現了41次,出現的次數最多,
∴這組數據的眾數為2.
∵將這組數據按從小到大的順序排列,其中處于中間的兩個數都是2,有![]() ,
,
∴這組數據的中位數為2.
(Ⅲ)估計這1500名學生一個月閱讀2本課外書的人數約為:
![]() (本).
(本).


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】函數y=![]() 和y=
和y=![]() 在第一象限內的圖象如圖,點P是y=
在第一象限內的圖象如圖,點P是y=![]() 的圖象上一動點,PC⊥x軸于點C,交y=
的圖象上一動點,PC⊥x軸于點C,交y=![]() 的圖象于點B.給出如下結論:①△ODB與△OCA的面積相等;②PA與PB始終相等;③四邊形PAOB的面積大小不會發生變化;④CA=
的圖象于點B.給出如下結論:①△ODB與△OCA的面積相等;②PA與PB始終相等;③四邊形PAOB的面積大小不會發生變化;④CA=![]() AP.其中所有正確結論的序號是( )
AP.其中所有正確結論的序號是( )
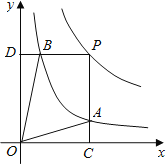
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀與應用:同學們,你們已經知道![]() ,即
,即![]() .所以
.所以![]() (當且僅當
(當且僅當![]() 時取等號).
時取等號).
閱讀1:若![]() 為實數,且
為實數,且![]() (當且僅當
(當且僅當![]() 時取等號).
時取等號).
閱讀2:若函數![]() (
(![]() ,
,![]() ,
,![]() 為常數).由閱讀1結論可知:
為常數).由閱讀1結論可知:![]() 即
即![]() ,∴當
,∴當![]() 即
即![]() 時,函數
時,函數![]() 的最小值為
的最小值為![]() .
.
閱讀理解上述內容,解答下列問題:
問題1:若函數![]() ,則
,則![]() = 時,函數
= 時,函數![]() 的最小值為 .
的最小值為 .
問題2:已知一個矩形的面積為4,其中一邊長為![]() ,則另一邊長為
,則另一邊長為![]() ,周長為
,周長為![]() ,求當
,求當![]() 時,矩形周長的最小值為 .
時,矩形周長的最小值為 .
問題3:求代數式![]() 的最小值.
的最小值.
問題4:建造一個容積為8立方米,深2米的長方體無蓋水池,池底和池壁的造價分別為每平方米![]() 米,水池總造價為
米,水池總造價為![]() (元),求當
(元),求當![]() 為多少時,水池總造價
為多少時,水池總造價![]() 最低?最低是多少?
最低?最低是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在ABCD中,已知AB=6,BE平分∠ABC交AD邊于點E,點E將AD分為1:3兩部分,則AD的長為( )
A. 8或24B. 8C. 24D. 9或24
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形![]() 是平行四邊形,點
是平行四邊形,點![]() 和
和![]() 在
在![]() 軸上,且
軸上,且![]() 為坐標原點,點
為坐標原點,點![]() ,和點
,和點![]() ,連接
,連接![]() 并延長交
并延長交![]() 軸于點
軸于點![]() .
.
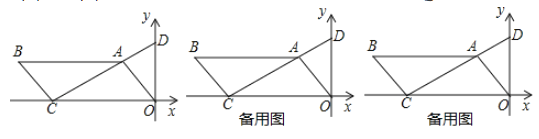
(1)求直線![]() 的解析式;
的解析式;
(2)若點![]() 從
從![]() 出發以2個單位/秒的速度沿
出發以2個單位/秒的速度沿![]() 軸向右運動,同時點
軸向右運動,同時點![]() 從
從![]() 出發,以1個單位/秒的速度沿
出發,以1個單位/秒的速度沿![]() 軸向左運動,過點
軸向左運動,過點![]() ,
,![]() 分別作
分別作![]() 軸的垂線交射線
軸的垂線交射線![]() 和射線
和射線![]() 分別于點
分別于點![]() ,
,![]() ,請猜想四邊形
,請猜想四邊形![]() 的形狀,(點
的形狀,(點![]() ,
,![]() 重合除外),并證明你的結論.
重合除外),并證明你的結論.
(3)在(2)的條件下,當點![]() 運動多少秒時,四邊形
運動多少秒時,四邊形![]() 是正方形?直接寫出結論.
是正方形?直接寫出結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,![]() 為原點,拋物線
為原點,拋物線![]() 經過點
經過點![]() ,對稱軸為直線
,對稱軸為直線![]() ,點
,點![]() 關于直線
關于直線![]() 的對稱點為點
的對稱點為點![]() .過點
.過點![]() 作直線
作直線![]() 軸,交
軸,交![]() 軸于點
軸于點![]() .
.
(Ⅰ)求該拋物線的解析式及對稱軸;
(Ⅱ)點![]() 在
在![]() 軸上,當
軸上,當![]() 的值最小時,求點
的值最小時,求點![]() 的坐標;
的坐標;
(Ⅲ)拋物線上是否存在點![]() ,使得
,使得![]() ,若存在,求出點
,若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了推動陽光體育運動的廣泛開展,引導學生走向操場、走進大自然、走到陽光下,積極參加體育鍛煉,學校準備購買一批運動鞋供學生借用.現從各年級隨機抽取了部分學生的鞋號,繪制出如下的統計圖①和圖②,請根據相關信息,解答下列問題:
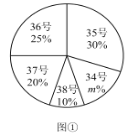
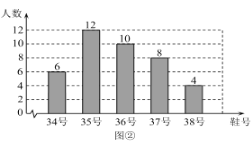
(Ⅰ)本次接受隨機抽樣調查的學生人數為________,圖①中![]() 的值為________;
的值為________;
(Ⅱ)求本次調查獲取的樣本數據的眾數和中位數;
(Ⅲ)根據樣本數據,若學校計劃購買150雙運動鞋,建議購買35號運動鞋多少雙?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 表示以
表示以![]() 為自變量的函數,則
為自變量的函數,則![]() 表示當
表示當![]() 時
時![]() 函數的值.例如,一次函數
函數的值.例如,一次函數![]() 記作
記作![]() ,當
,當![]() 時,函數值
時,函數值![]() .現給出新定義:對于函數
.現給出新定義:對于函數![]() ,若存在實數
,若存在實數![]() ,使得成立
,使得成立![]() ,則稱點
,則稱點![]() 是函數
是函數![]() 的“奇妙點”.
的“奇妙點”.
(1)求函數![]() 的“奇妙點”;
的“奇妙點”;
(2)當![]() 為何值時,函數
為何值時,函數![]() 存在“奇妙點”?
存在“奇妙點”?
(3)若二次函數![]() 有且只有一個“奇妙點”
有且只有一個“奇妙點”![]() ,其圖象與
,其圖象與![]() 軸交于
軸交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),
的左側),![]() 是
是![]() 軸上一動點.當
軸上一動點.當![]() 的周長最短時,求點
的周長最短時,求點![]() 的坐標及
的坐標及![]() 的周長.
的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
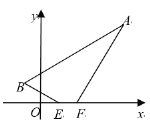
【題目】如圖,在直角坐標系中,已知A(4,4),B(-1,1),EF=1,線段EF在x軸上平移,當四邊形ABEF的周長最小時,點E坐標是__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com