
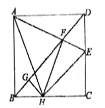
【題目】如圖,在正方形![]() 中,
中,![]() ,
,![]() 為
為![]() 上一動點,
上一動點,![]() 交
交![]() 于
于![]() ,過
,過![]() 作
作![]() 交
交![]() 于點
于點![]() ,過
,過![]() 作
作![]() 于
于![]() ,連結
,連結![]() .在以下四個結論中:①
.在以下四個結論中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 的周長為12.其中正確的結論有__________(填序號)
的周長為12.其中正確的結論有__________(填序號)
【答案】②④
【解析】
①作輔助線,延長HF交AD于點L,連接CF,通過證明△ADF≌△CDF,可得:AF=CF,故需證明FC=FH,可證:AF=FH;
②由FH⊥AE,AF=FH,可得:∠HAE=45°;
③F是動點,CF的長度不是定值;
④作輔助線,延長AD至點M,使AD=DM,過點C作CI//HL,則IL=HC,可證AL=HE,再根據△MEC≌△MIC,可證:CE=IM,故△CEH的周長為邊AM的長,為定值.
解:①連接FC,延長HF交AD于點L,

∵BD為正方形ABCD的對角線,
∴∠ADB=∠CDF=45°.
∵AD=CD,DF=DF,
∴△ADF≌△CDF.
∴FC=AF,∠ECF=∠DAF.
∵∠ALH+∠LAF=90°,
∴∠LHC+∠DAF=90°.
∵∠ECF=∠DAF,
∴∠FHC=∠FCH,
∴FH=FC.
∴FH=AF..故①錯誤,
②∵FH⊥AE,FH=AF,
∴∠HAE=45°.
③∵F是動點,CF的長度不是定值,本選項錯誤;
④延長AD至點M,使AD=DM,過點C作CI//HL,則:LI=HC,
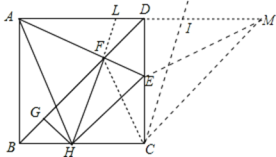
根據△MEC≌△CIM,可得:CE=IM,
同理,可得:AL=HE,
∴HE+HC+EC=AL+LI+IM=AM=12.
∴△CEH的周長為12,為定值.
故②④結論都正確.
故答案為②④.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案 目標測試系列答案
目標測試系列答案科目:初中數學 來源: 題型:
【題目】如圖,一次函數 ![]() 分別交y軸、x 軸于A、B兩點,拋物線
分別交y軸、x 軸于A、B兩點,拋物線 ![]() 過A、B兩點.
過A、B兩點.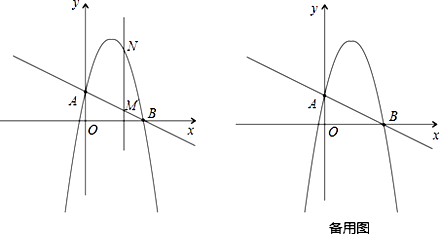
(1)求這個拋物線的解析式;
(2)作垂直x軸的直線x=t,在第一象限交直線AB于點M,交這個拋物線于點N.求當t 取何值時,MN有最大值?最大值是多少?
(3)在(2)的情況下,以A、M、N、D為頂點作平行四邊形,求第四個頂點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》是我國古代數學的經典著作,書中有一個問題:“今有黃金九枚,白銀一十一枚,稱之重適等.交易其一,金輕十三兩.問金、銀一枚各重幾何?”.意思是:甲袋中裝有黃金9枚(每枚黃金重量相同),乙袋中裝有白銀11枚(每枚白銀重量相同),稱重兩袋相等.兩袋互相交換1枚后,甲袋比乙袋輕了13兩(袋子重量忽略不計).問黃金、白銀每枚各重多少兩?設每枚黃金重x兩,每枚白銀重y兩,根據題意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c+2的圖象如圖,頂點為(-1,0),下列結論:①abc<0;②b2-4ac=0;③a>2;④4a-2b+c>0.其中正確結論的個數是( )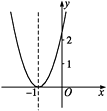
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角三角形△ABC中,∠C=90°,AD平分∠BAC交BC于點D,BE平分∠ABC交AC于點E,AD、BE相交于點F,過點D作DG∥AB,過點B作BG⊥DG交DG于點G.下列結論:①∠AFB=135°;②∠BDG=2∠CBE;③BC平分∠ABG;④∠BEC=∠FBG.其中正確的是_________.(填序號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2018年宜賓市創建全國文明城市的過程中,某小區決定購買文明用語提示牌和文明信息公示欄.若購買2個提示牌和3個公示欄需要510元;購買3個提示牌和5個公示欄需要840元.
(1)求提示牌和公示欄的單價各是多少元?
(2)若該小區購買提示牌和公示欄共50個,要求購買公示欄至少12個,且總費用不超過3200元.請你列舉出所有購買方案,并指出哪種方案費用最少,最少費用為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某聯歡會上有一個有獎游戲,規則如下:有5張紙牌,背面都是喜羊羊頭像,正面有2張是笑臉,其余3張是哭臉.現將5張紙牌洗勻后背面朝上擺放到桌上,若翻到的紙牌中有笑臉就有獎,沒有笑臉就沒有獎.
(1)小芳獲得一次翻牌機會,她從中隨機翻開一張紙牌.小芳得獎的概率是.
(2)小明獲得兩次翻牌機會,他同時翻開兩張紙牌.小明認為這樣得獎的概率是小芳的兩倍,你贊同他的觀點嗎?請用樹形圖或列表法進行分析說明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖, 在□ABCD中,點E、F是AD、BC的中點,連接BE、DF.
(1)求證:BE=DF.
(2)若BE平分∠ABC且交邊AD于點E,AB=6cm,BC=10cm,試求線段DE的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com