【題目】2018年宜賓市創建全國文明城市的過程中，某小區決定購買文明用語提示牌和文明信息公示欄.若購買2個提示牌和3個公示欄需要510元；購買3個提示牌和5個公示欄需要840元.
（1）求提示牌和公示欄的單價各是多少元？
（2）若該小區購買提示牌和公示欄共50個，要求購買公示欄至少12個，且總費用不超過3200元.請你列舉出所有購買方案，并指出哪種方案費用最少，最少費用為多少元？
【答案】（1）提示牌和公示欄的單價各是30元,150元；（2）有三種方案：方案1：購買12個公示欄，38個提示牌；方案2：購買13個公示欄，37個提示牌；方案3：購買14個公示欄，36個提示牌. 當購買12個公示欄，38個提示牌時，費用最少，最少費用為
元.
【解析】
（1）設提示牌和公示欄的單價各是
元,
元，根據“①購買2個提示牌和3個公示欄需要510元；②購買3個提示牌和5個公示欄需要840元”列出方程組，解方程組即可求解；（2）設購買
個公示欄，則購買提示牌（
）個，根據“購買公示欄至少12個，且總費用不超過3200元”列出不等式組，解不等式組求m的取值范圍，由于m取整數，由此即可確定m的值，從而確定購買方案，再計算最少費用即可.
（1）解：設提示牌和公示欄的單價各是元,元.
由題得：
解之得：
答：提示牌和公示欄的單價各是30元,150元.
（2）設購買個公示欄，則購買提示牌（）個.
由題：
不等式組解集為：
∵是整數
∴
，共有三種方案.
方案1：購買12個公示欄，38個提示牌；
方案2：購買13個公示欄，37個提示牌；
方案3：購買14個公示欄，36個提示牌.
當購買12個公示欄，38個提示牌時，費用最少，最少費用為：
元.
科目：初中數學 來源： 題型：
【題目】已知AB是⊙O的直徑，C、E是⊙O上的點， CD⊥AB，EF⊥AB，垂足分別為D、F，過點E作 EG⊥0C，垂足為G，延長EG交OA于H。
求證：
（1）HO·HF=HG·HE；
（2）FG=CD
查看答案和解析>>
科目：初中數學 來源： 題型：
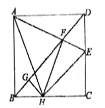
【題目】如圖，在正方形
中，
，
為
上一動點，
交
于
，過作
交
于點
，過作
于
，連結
．在以下四個結論中：①
；②
；③
；④
的周長為12．其中正確的結論有__________（填序號）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀理解：
對于任意一個三位數正整數n，如果n的各個數位上的數字互不相同，且都不為零，那么稱這個數為“陌生數”，將一個“陌生數”的三個數位上的數字交換順序，可以得到5個不同的新“陌生數”，把這6個陌生數的和與111的商記為M(n).例如n=123，可以得到132.213.231.312.321這5個新的“陌生數”，這6個“陌生數”的和為123＋132＋213＋231＋312＋321=1332，因為
，所以M(123)=12.
(1)計算：M(125)和M(361)的值；
(2)設s和t都是“陌生數”，其中4和2分別是s的十位和個位上的數字，2和5分別是t的百位和個位上的數字，且t的十位上的數字比s的百位上的數字小2；規定：
.若
，則k的值是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在銳角△ABC中，∠BAC＝60，BD、CE為高，F為BC的中點，連接DE、DF、EF，則結論：①DF＝EF；②AD∶AB＝AE∶AC；③△DEF是等邊三角形；④BE＋CD＝BC；⑤當∠ABC＝45時，BE＝
DE中，一定正確的有 ．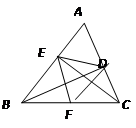 
查看答案和解析>>
科目：初中數學 來源： 題型：
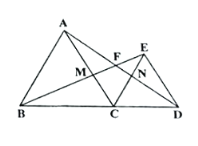
【題目】如圖，己知點C是線段BD上一點，以BC、 DC為一邊在BD的同一側作等邊△ABC和等邊△ECD,連接AD, BE相交于點F, AC和BE交于點M, AD, CE交于點N,(注：等邊三角形的每一個內角都等于60° )
(1) 求證： AD=BE
(2) 線段CM與CN相等嗎?請證明你的結論。
(3) 求∠BFD的度數。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，拋物線y1= 
（x+1）2+1與y2=a（x﹣4）2﹣3交于點A（1，3），過點A作x軸的平行線，分別交兩條拋物線于B、C兩點，且D、E分別為頂點．則下列結論： ①a= 
；②AC=AE；③△ABD是等腰直角三角形；④當x＞1時，y1＞y2
其中正確結論的個數是（ ）
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
