
【題目】對于直角坐標系 xOy 中的點P和⊙C,給出如下定義:若⊙C上存在兩個點A,B,使得點P在射線BC上,且∠APB=![]() ∠ACB(0°<∠ACB<180°),則稱P為⊙C的依附點.
∠ACB(0°<∠ACB<180°),則稱P為⊙C的依附點.
(1)當⊙O的半徑為1時
①已知點D(﹣1,0),E(0,﹣2),F(2.5,0),在點D,E,F中,⊙O的依附點是___;
②點T在直線y=![]() x上,若T為⊙O的依附點,求點T的橫坐標t的取值范圍;
x上,若T為⊙O的依附點,求點T的橫坐標t的取值范圍;
(2)⊙C的圓心在x軸上,半徑為1,直線 y=﹣2x+2與x軸、y 軸分別交于點M、N,若線段MN上的所有點都是⊙C 的依附點,請求出圓心C的橫坐標n的取值范圍.
【答案】(1)①![]() 、
、![]() ;②
;②![]() 或
或![]() ;
;
(2)![]() 或
或![]() .
.
【解析】
(1)①如圖1中,根據![]() 為
為![]() 的依附點,可知:當
的依附點,可知:當![]() 為
為![]() 的半徑)時,點
的半徑)時,點![]() 為
為![]() 的依附點,由此即可判斷.
的依附點,由此即可判斷.
②分兩種情形:點![]() 在第一象限或點
在第一象限或點![]() 在第三象限分別求解即可.
在第三象限分別求解即可.
(2)分兩種情形:點![]() 在點
在點![]() 的右側,點
的右側,點![]() 在點
在點![]() 的左側分別求解即可解決問題.
的左側分別求解即可解決問題.
解:(1)①如圖1中,根據![]() 為
為![]() 的依附點,可知:當
的依附點,可知:當![]() 為
為![]() 的半徑)時,點
的半徑)時,點![]() 為
為![]() 的依附點.
的依附點.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 點
點![]() ,
,![]() 是
是![]() 的依附點,
的依附點,
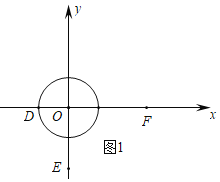
故答案為:![]() 、
、![]() ;
;
(2)如圖2,
![]() 點
點![]() 在直線
在直線![]() 上,
上,
![]() 點
點![]() 在第一象限或第三象限,直線
在第一象限或第三象限,直線![]() 與
與![]() 軸所夾的銳角為
軸所夾的銳角為![]() ,
,
當點![]() 在第一象限,當
在第一象限,當![]() 時,作
時,作![]() 軸垂足為C,易求點
軸垂足為C,易求點![]() ,
,![]() ;
;
當![]() 時,作
時,作![]() 軸,易求
軸,易求![]() ,
,![]() ,
,
![]() 滿足條件的點
滿足條件的點![]() 的橫坐標
的橫坐標![]() 的取值范圍
的取值范圍![]() ,
,
當點![]() 在第三象限,同理可得滿足條件的點
在第三象限,同理可得滿足條件的點![]() 的橫坐標
的橫坐標![]() 的取值范圍
的取值范圍![]() ,
,
綜上所述:滿足條件的點![]() 的橫坐標
的橫坐標![]() 的取值范圍:
的取值范圍:![]() 或
或![]() ,
,
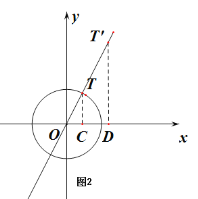
(3)![]() 由題意直線 y=﹣2x+2與x軸、y 軸分別交點坐標為:
由題意直線 y=﹣2x+2與x軸、y 軸分別交點坐標為:![]() ,
,![]() .
.
如圖![]() 中,當點
中,當點![]() 在點
在點![]() 的右側時,
的右側時,
當![]() 時,
時,![]() ,此時
,此時![]() ,
,![]() ;
;
當![]() 時,此時
時,此時![]() .
.
![]() 滿足條件的
滿足條件的![]() 的值的范圍為
的值的范圍為![]() .
.
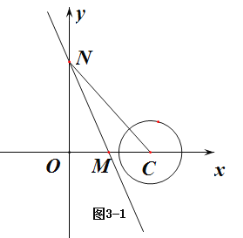
如圖![]() 中,當點
中,當點![]() 在點
在點![]() 的右側時,
的右側時,
當![]() 與直線
與直線![]() 相切時,易知
相切時,易知![]() ;
;
當![]() 時,
時,![]() .
.
![]() 滿足條件的n的值的范圍為
滿足條件的n的值的范圍為![]() .
.
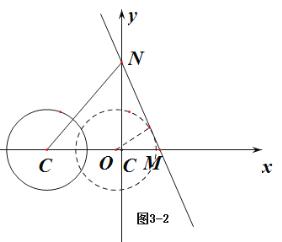
綜上所述,滿足條件的![]() 的值的范圍為:
的值的范圍為:![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,將矩形ABCD沿AF折疊,使點D落在BC邊的點E處,過點E作EG∥CD交AF于點G,連接DG.
(1)求證:四邊形EFDG是菱形;
(2)求證:EG2=![]() GF
GF![]() AF;
AF;
(3)若AB=4,BC=5,求GF的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用一張斜邊![]() 長為
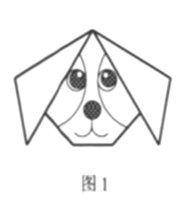
長為![]() 的等腰直角三角形紙片進行折“狗臉”活動(如圖1所示) .第一步,如圖2,沿
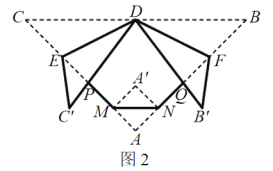
的等腰直角三角形紙片進行折“狗臉”活動(如圖1所示) .第一步,如圖2,沿![]() 向后折一個面積為1的等腰直角三角形
向后折一個面積為1的等腰直角三角形![]() ;第二步,在直角邊
;第二步,在直角邊![]() .上各取一點
.上各取一點![]() 為
為![]() 的中點,將
的中點,將![]() 分別沿
分別沿![]() 折疊,使得點
折疊,使得點![]() 對應點
對應點![]() 落在直線
落在直線![]() 上,
上,![]() 交
交![]() 于點
于點![]() 交
交![]() 于點
于點![]() ,則“狗臉”(圖形
,則“狗臉”(圖形![]() )的面積為__________.
)的面積為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一次函數y=kx+b的圖象與反比例函數![]() 的圖象交于A,B兩點,且點A的橫坐標和點B的縱坐標都是﹣2,
的圖象交于A,B兩點,且點A的橫坐標和點B的縱坐標都是﹣2,
求:(1)一次函數的解析式;
(2)△AOB的面積;
(3)直接寫出一次函數的函數值大于反比例函數的函數值時x的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是小星同學設計的“過直線外一點作已知直線的平行線”的尺規作圖過程: 已知:如圖,直線 l 和直線 l 外一點 A
求作:直線 AP,使得 AP∥l

作法:如圖
①在直線 l 上任取一點 B(AB 與 l 不垂直),以點 A 為圓心,AB 為半徑作圓,與直線 l
交于點 C.
②連接 AC,AB,延長 BA 到點 D;
③作∠DAC的平分線AP.
所以直線AP就是所求作的直線,
根據小星同學設計的尺規作圖過程,完成下面的證明證明:
∵AB=AC,
∴∠ABC=∠ACB_________(填推理的依據)
∵∠DAC 是△ABC 的外角,∴∠DAC=∠ABC+∠ACB
∴∠DAC=2∠ABC
∵AP 平分∠DAC,
∴∠DAC=2∠DAP
∴∠DAP=∠ABC
∴AP∥l_________(填推理的依據)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,O為AC的中點,直線EF經過點O,并且與AB交于點E,與DC交于點F,∠DFE=∠BFE.
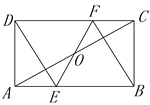
(1)求證:四邊形DEBF是菱形;
(2)若AD=4,AB=8,則線段EF的長是_______.(直接寫出答案即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
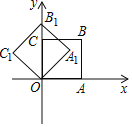
【題目】如圖,在平面直角坐標系中,將正方形OABC繞點O逆時針旋轉45°后得到正方形OA1B1C1,依此方式,繞點O連續旋轉2018次得到正方形OA2018B2018C2018,如果點A的坐標為(1,0),那么點B2018的坐標為( )
A. (1,1) B. (0,![]() ) C. (
) C. (![]() ) D. (﹣1,1)
) D. (﹣1,1)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知點A的坐標是(4,0),并且OA=OC=4OB,動點P在過A,B,C三點的拋物線上.
(1)求拋物線的解析式;
(2)是否存在點P,使得△ACP是以AC為直角邊的直角三角形?若存在,求出所有符合條件的點P的坐標;若不存在,說明理由;
(3)過動點P作PE垂直于y軸于點E,交直線AC于點D,過點D作x軸的垂線.垂足為F,連接EF,以線段EF的中點G為圓心,以EF為直徑作⊙G,當⊙G最小時,求出點P的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com