
【題目】已知關于x的一元二次方程mx2+(3m+1)x+3=0.
(1)求證:該方程有兩個實數根;
(2)如果拋物線y=mx2+(3m+1)x+3與x軸交于A、B兩個整數點(點A在點B左側),且m為正整數,求此拋物線的表達式;
(3)在(2)的條件下,拋物線y=mx2+(3m+1)x+3與y軸交于點C,點B關于y軸的對稱點為D,設此拋物線在﹣3≤x≤﹣![]() 之間的部分為圖象G,如果圖象G向右平移n(n>0)個單位長度后與直線CD有公共點,求n的取值范圍.
之間的部分為圖象G,如果圖象G向右平移n(n>0)個單位長度后與直線CD有公共點,求n的取值范圍.
【答案】(1)證明見解析;(2)y=x2+4x+3;(3)![]() ≤n≤4;
≤n≤4;
【解析】
(1)先求出根的判別式△,判斷△的取值范圍,即可得證;
(2)根據求根公式表示出兩根,由題意,求出m的值,可得拋物線的解析式;
(3)點求出點A,B,C,D的坐標,根據待定系數法求出直線CD的解析式,設平移后,點A,E的對應點分別為A′(﹣3+n,0),E′(﹣![]() +n,
+n,![]() ),根據點在直線上,求出取值范圍即可.
),根據點在直線上,求出取值范圍即可.
(1)由根的判別式,可得:△=(3m+1)2﹣4×m×3=(3m﹣1)2.
∵(3m﹣1)2≥0,∴△≥0,∴原方程有兩個實數根;
(2)令y=0,那么mx2+(3m+1)x+3=0,解得:x1=﹣3,x2=﹣![]() .
.
∵拋物線與x軸兩個交點的橫坐標均為整數,且m為正整數,∴m=1,∴拋物線的解析式為:y=x2+4x+3;
(3)如圖,∵當x=0時,y=3,∴C(0,3).
∵當y=0時,x1=﹣3,x2=﹣1.
又∵點A在點B的左側,∴A(﹣3,0),B(﹣1,0).
∵點D與點B關于y軸對稱,∴D(1,0),設直線CD的解析式為:y=kx+b,∴![]() ,解得:
,解得:![]() ,∴直線CD的表達式為:y=﹣3x+3.
,∴直線CD的表達式為:y=﹣3x+3.
又∵當x=﹣![]() 時,y=
時,y=![]() ,∴點E(﹣
,∴點E(﹣![]() ),∴平移后,點A,E的對應點分別為A′(﹣3+n,0),E′(﹣
),∴平移后,點A,E的對應點分別為A′(﹣3+n,0),E′(﹣![]() +n,
+n,![]() ),當直線y=﹣3x+3經過點A′(﹣3+n,0)時,得:﹣3(﹣3+n)+3=0,解得:n=4,當直線y=﹣3x+3經過點E′(﹣
),當直線y=﹣3x+3經過點A′(﹣3+n,0)時,得:﹣3(﹣3+n)+3=0,解得:n=4,當直線y=﹣3x+3經過點E′(﹣![]() +n,
+n,![]() ),時,得:﹣3(﹣
),時,得:﹣3(﹣![]() +n)+3=
+n)+3=![]() ,解得:n=
,解得:n=![]() ,∴n的取值范圍是
,∴n的取值范圍是![]() ≤n≤4.
≤n≤4.


科目:初中數學 來源: 題型:
【題目】用一條24cm的細繩圍成一個等腰三角形。
(1)如果腰長是底邊的2倍,那么各邊的長是多少?
(2)能圍成有一邊長為4cm的等腰三角形嗎?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形ABCD的邊長AB=2,E為AB的中點,F為BC的中點,AF分別與DE、BD相交于點M,N,則MN的長為( )
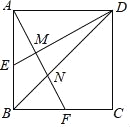
A. ![]() B.
B. ![]() ﹣1 C.
﹣1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,給出以下四個結論,其中不正確的結論是( )
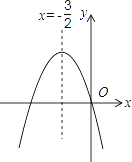
A. abc=0 B. a+b+c>0 C. 3a=b D. 4ac﹣b2<0
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們定義:如果兩個等腰三角形的頂角相等,且項角的頂點互相重合,則稱此圖形為“手拉手全等模型”.因為頂點相連的四條邊,形象的可以看作兩雙手,所以通常稱為“手拉手模型”.例如,如(1),![]() 與
與![]() 都是等腰三角形,其中
都是等腰三角形,其中![]() ,則△ABD≌△ACE(SAS).
,則△ABD≌△ACE(SAS).
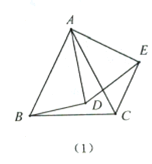
(1)熟悉模型:如(2),已知![]() 與
與![]() 都是等腰三角形,AB=AC,AD=AE,且
都是等腰三角形,AB=AC,AD=AE,且![]() ,求證:
,求證:![]() ;
;
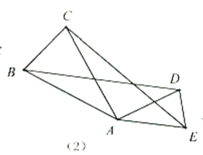
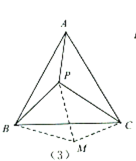
(2)運用模型:如(3),![]() 為等邊
為等邊![]() 內一點,且
內一點,且![]() ,求
,求![]() 的度數.小明在解決此問題時,根據前面的“手拉手全等模型”,以
的度數.小明在解決此問題時,根據前面的“手拉手全等模型”,以![]() 為邊構造等邊
為邊構造等邊![]() ,這樣就有兩個等邊三角形共頂點
,這樣就有兩個等邊三角形共頂點![]() ,然后連結
,然后連結![]() ,通過轉化的思想求出了
,通過轉化的思想求出了![]() 的度數,則
的度數,則![]() 的度數為 度;
的度數為 度;
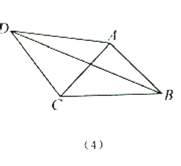
(3)深化模型:如(4),在四邊形![]() 中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,求
中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,A(-1,5),B(﹣1,0),C(﹣4,3).
(1)在圖中畫出△ABC關于y軸對稱的圖形△A1B1C1;(其中A1、B1、C1分別是A、B、C的對應點,不寫畫法.)
(2)寫出點A1、B1、C1的坐標;
(3)求出△A1B1C1的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,CD是經過![]() 頂點C的一條直線,且直線CD經過
頂點C的一條直線,且直線CD經過![]() 的內部,點E,F在射線CD上,已知
的內部,點E,F在射線CD上,已知![]() 且
且![]() .
.
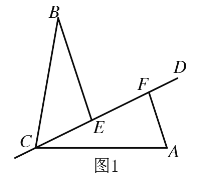
(1)如圖1,若![]() ,
,![]() ,問
,問![]() ,成立嗎?說明理由.
,成立嗎?說明理由.
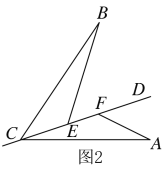
(2)將(1)中的已知條件改成![]() ,
,![]() (如圖2),問
(如圖2),問![]() 仍成立嗎?說明理由.
仍成立嗎?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠A=∠D=90°,點E、F在線段BC上,DE與AF交于點O,且AB=DC,BE=CF.求證:
(1)AF=DE
(2)若OP⊥EF,求證:OP平分∠EOF.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將正面分別寫著數字1,2,3的三張卡片(注:這三張卡片的形狀、大小、質地,顏色等其他方面完全相同,若背面上放在桌面上,這三張卡片看上去無任何差別)洗勻后,背面向上放在桌面上,從中先隨機抽取一張卡片,記該卡片上的數字為x,再把剩下的兩張卡片洗勻后,背面向上放在桌面上,再從這兩張卡片中隨機抽取一張卡片,記該卡片上的數字為y.
(1)用列表法或樹狀圖法(樹狀圖也稱樹形圖)中的一種方法,寫出(x,y)所有可能出現的結果.
(2)求取出的兩張卡片上的數字之和為偶數的概率P.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com