【題目】如圖，四邊形ABCD 中，AB=AD，點B關于AC的對稱點B′恰好落在CD上，若∠BAD=
，則∠ACB的度數為（ ）
A. 
α B. 90°-α C. 45° D. α-45°
【答案】B
【解析】
連接AB'，BB'，過A作AE⊥CD于E，依據∠BAC=∠B'AC，∠DAE=∠B'AE，即可得出∠CAE=
∠BAD=
，再根據四邊形內角和以及三角形外角性質，即可得到∠ACB=∠ACB'=90°﹣．
如圖，連接AB'，BB'，過A作AE⊥CD于E．
∵點B關于AC的對稱點B'恰好落在CD上，∴AC垂直平分BB'，∴AB=AB'，∴∠BAC=∠B'AC．
∵AB=AD，∴AD=AB'．
又∵AE⊥CD，∴∠DAE=∠B'AE，∴∠CAE=∠BAD=．
又∵∠AEB'=∠AOB'=90°，∴四邊形AOB'E中，∠EB'O=180°﹣，∴∠ACB'=∠EB'O﹣∠COB'=180°﹣﹣90°=90°﹣，∴∠ACB=∠ACB'=90°﹣．
故選B．
名師導航單元期末沖刺100分系列答案
名校名卷單元同步訓練測試題系列答案科目：初中數學 來源： 題型：
【題目】如圖，為測量一座山峰CF的高度，將此山的某側山坡劃分為AB和BC兩段，每一段山坡近似是“直”的，測得坡長AB=800米，BC=200米，坡角∠BAF=30°，∠CBE=45°．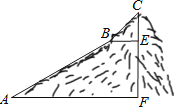
（1）求AB段山坡的高度EF；
（2）求山峰的高度CF．（ 
1.414，CF結果精確到米）
查看答案和解析>>
科目：初中數學 來源： 題型：
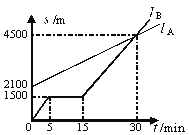
【題目】A、B兩名同學在同一個學校上學，B同學上學的路上經過A同學家。A同學步行，B同學騎自行車，某天，A，B兩名同學同時從家出發到學校，如圖，
A表示A同學離B同學家的路程
A(m)與行走時間
(min)之間的函數關系圖象，B表示B同學離家的路程B(m)與行走時間(min)之間的函數關系圖象.
（1）A，B兩名同學的家相距________m.
（2）B同學走了一段路后，自行車發生故障，進行修理，修理自行車所用的時間是 _____min.
（3）B同學出發后______min與A同學相遇.
（4）求出A同學離B同學家的路程A與時間的函數關系式.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知：E是∠AOB的平分線上一點，EC⊥OB，ED⊥OA，C、D是垂足，連接CD，且交OE于點F.
（1）求證：OE是CD的垂直平分線.
（2）若∠AOB=60，請你探究OE，EF之間有什么數量關系？并證明你的結論。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AD是△ABC的中線，∠ADC=45°，把△ADC沿著直線AD對折，點C落在點E的位置．如果BC=6，那么線段BE的長度為（ ） 
A.6
B.6 
C.2 
D.3
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，∠A=∠B，AE=BE，點D在AC邊上，∠1=∠2，AE和BD相交于點O．
（1）求證：△AEC≌△BED；
（2）若∠1=42°，求∠BDE的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】從分別標有數﹣3，﹣2，﹣1，0，1，2，3的七張沒有明顯差別的卡片中，隨機抽取一張，所抽卡片上的數的絕對值不小于2的概率是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知AB為⊙O的直徑，AC為⊙O的切線，OC交⊙O于點D，BD的延長線交AC于點E．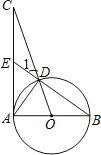
（1）求證：∠1=∠CAD；
（2）若AE=EC=2，求⊙O的半徑．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
