
【題目】操作與思考:一張邊長為a的正方形桌面,因為實際需要,需將正方形邊長增加b,從而得到一個更大的正方形,木工師傅設計了如圖所示的方案:
(1)方案中大正方形的邊長都是 ,所以面積為 ;
(2)小明還發現:方案中大正方形的面積還可以用四塊小四邊形的面積和來表示 ;
(3)你有什么發現,請用數學式子表達 ;
(4)利用(3)的結論計算20.182+2×20.18×19.82+19.822的值.

【答案】(1) (a+b),(a+b)2;(2) (a2+2ab+b2);(3) (a+b)2=a2+2ab+b2;(4)1600
【解析】
(1)根據圖形得出正方形的邊長,再利用正方形的面積公式即可得;
(2)將四個小四邊形的面積相加,再合并同類項即可得;
(3)由大正方形面積不變可得等式;
(4)利用所得等式將原式變形為(20.18+19.82)2,再進一步計算可得.
解:(1)方案中大正方形的邊長都是(a+b),所以面積為(a+b)2,
故答案為:(a+b),(a+b)2;
(2)方案中大正方形的面積還可以用四塊小四邊形的面積和來表示:a2+ab+ab+b2=a2+2ab+b2,
故答案為:(a2+2ab+b2);
(3)根據大正方形的面積不變可知(a+b)2=a2+2ab+b2,
故答案為:(a+b)2=a2+2ab+b2.
(4)20.182+2×20.18×19.82+19.822
=(20.18+19.82)2
=402
=1600.


 名師點撥卷系列答案
名師點撥卷系列答案 英才計劃期末調研系列答案
英才計劃期末調研系列答案科目:初中數學 來源: 題型:
【題目】某商場銷售甲、乙兩種品牌的智能手機,這兩種手機的進價和售價如下表:
甲 | 乙 | |
進價(元/部) | 4000 | 2500 |
售價(元/部) | 4300 | 3000 |
該商場計劃購進兩種手機若干部,共需15.5萬元,預計全部銷售后可獲毛利潤共2.1萬元.
(毛利潤=(售價﹣進價)×銷售量)
(1)該商場計劃購進甲、乙兩種手機各多少部?
(2)通過市場調研,該商場決定在原計劃的基礎上,減少甲種手機的購進數量,增加乙種手機的購進數量.已知乙種手機增加的數量是甲種手機減少的數量的2倍,而且用于購進這兩種手機的總資金不超過16萬元,該商場怎樣進貨,使全部銷售后獲得的毛利潤最大?并求出最大毛利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AD∥BC,且AD>BC,BC=6 cm,動點P,Q分別從A,C同時出發,P以1 cm/s的速度由A向D運動,Q以2cm/s的速度由C向B運動(Q運動到B時兩點同時停止運動),則________后四邊形ABQP為平行四邊形.
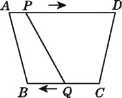
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P、Q分別是邊長為4cm的等邊△ABC邊AB、BC上的動點,點P從頂點A,點Q從頂點B同時出發,且速度都為1cm/s,連接AQ、CP交于點M,下面四個結論:①△ABQ≌△CAP;;②∠CMQ的度數不變,始終等于60°③BP=CM;正確的有幾個( )
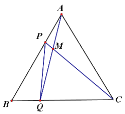
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某日王老師佩戴運動手環進行快走鍛煉,兩次鍛煉后數據如表.與第一次鍛煉相比,王老師第二次鍛煉步數增長的百分率是其平均步長減少的百分率的3倍.設王老師第二次鍛煉時平均步長減少的百分率為x(0<x<0.5).
項目 | 第一次鍛煉 | 第二次鍛煉 |
步數(步) | 10000 | ① |
平均步長(米/步) | 0.6 | ② |
距離(米) | 6000 | 7020 |
注:步數×平均步長=距離.
(1)根據題意完成表格填空;
(2)求x;
(3)王老師發現好友中步數排名第一為24000步,因此在兩次鍛煉結束后又走了500米,使得總步數恰好為24000步,求王老師這500米的平均步長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道:點A、B在數軸上分別表示有理數a、b,如圖A、B兩點之間的距離表示為AB,記作AB=|a﹣b|.回答下列問題:
(1)數軸上表示2和5兩點之間的距離是 ,數軸上表示1和﹣3的兩點之間的距離是 ;
(2)已知|a﹣3|=7,則有理數a= ;
(3)若數軸上表示數b的點位于﹣4與3的兩點之間,則|b﹣3|+|b+4|= .
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的三邊AB、BC、CA長分別是20、30、40,其三條角平分線將△ABC分為三個三角形,則S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,A(2,0)、B(0,3),過點B作直線∥x軸,點P(a,3)是直線上的動點,以AP為邊在AP右側作等腰RtAPQ,∠APQ=Rt∠,直線AQ交y軸于點C.
(1)當a=1時,則點Q的坐標為;
(2)當點P在直線上運動時,點Q也隨之運動.當a=時,AQ+BQ的值最小為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com