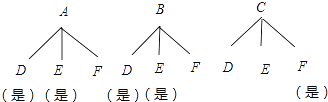
【題目】如圖，3×3的方格分為上中下三層，第一層有一枚黑色方塊甲，可在方格A、B、C中移動，第二層有兩枚固定不動的黑色方塊，第三層有一枚黑色方塊乙，可在方格D、E、F中移動，甲、乙移入方格后，四枚黑色方塊構成各種拼圖．
（1）若乙固定在E處，移動甲后黑色方塊構成的拼圖是軸對稱圖形的概率是________．
（2）若甲、乙均可在本層移動．
①用樹形圖或列表法求出黑色方塊所構拼圖是軸對稱圖形的概率________．
②黑色方塊所構拼圖是中心對稱圖形的概率是________．
【答案】（1）
；（2）①
；②
.
【解析】
（1）由乙固定在E處，移動甲后黑色方塊構成的拼圖一共有3種可能，其中有兩種情形是軸對稱圖形，所以若乙固定在E處，移動甲后黑色方塊構成的拼圖是軸對稱圖形的概率是；（2）①由樹狀圖得到黑色方塊所構拼圖是軸對稱圖形的概率；②黑色方塊所構拼圖中是中心對稱圖形有兩種情形，①甲在B處，乙在F處，②甲在C處，乙在E處，所以黑色方塊所構拼圖是中心對稱圖形的概率是．
（1）若乙固定在E處，移動甲后黑色方塊構成的拼圖一共有3種可能，其中有兩種情形是軸對稱圖形，所以若乙固定在E處，移動甲后黑色方塊構成的拼圖是軸對稱圖形的概率是 ．
故答案為．（2）①由樹狀圖可知，黑色方塊所構拼圖是軸對稱圖形的概率= ．
②黑色方塊所構拼圖中是中心對稱圖形有兩種情形，
甲在B處，乙在F處或甲在C處，乙在E處，
所以黑色方塊所構拼圖是中心對稱圖形的概率是 ．
故答案為 ．
科目：初中數學 來源： 題型：
【題目】已知：如圖1，OM是∠AOB的平分線，點C在OM上，OC＝5，且點C到OA的距離為3．過點C作CD⊥OA，CE⊥OB，垂足分別為D、E，易得到結論：OD+OE等于多少；
（1）把圖1中的∠DCE繞點C旋轉，當CD與OA不垂直時（如圖2），上述結論是否成立？并說明理由；
（2）把圖1中的∠DCE繞點C旋轉，當CD與OA的反向延長線相交于點D時：
①請在圖3中畫出圖形；
②上述結論還成立嗎？若成立，請給出證明；若不成立，請直接寫出線段OD、OE之間的數量關系，不需證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△PQN中，若∠P＝
∠Q＋α（0°＜α≤25°），則稱△PQN為“差角三角形”,且∠P是 ∠Q的“差角”.
（1）已知△ABC是等邊三角形，判斷△ABC是否為“差角三角形”，并說明理由；
（2）在△ABC中，∠C＝90°，50°≤∠B≤70°，判斷△ABC是否為“差角三角形”，若是，請寫出所有的“差角”并說明理由；若不是，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，E為AC的中點，AD平分∠BAC，BA：CA=2：3，AD與BE相交于點O，若△OAE的面積比△BOD的面積大1，則△ABC的面積是（ ）
A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD中，AB=AD，AC=5，∠DAB=∠DCB=90°，則四邊形ABCD的面積為（ ）
A. 15 B. 12.5 C. 14.5 D. 17
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，拋物線
與
軸交于
，
兩點（點在軸的正半軸上），與
軸交于點
，矩形
的一條邊
在線段
上，頂點
，
分別在線段
，
上．
求點，，的坐標；
若點
的坐標為
，矩形的面積為
，求關于
的函數表達式，并指出的取值范圍；
當矩形的面積取最大值時，
①求直線
的解析式；
②在射線上取一點
，使
，若點恰好落在該拋物線上，則
________．
查看答案和解析>>
科目：初中數學 來源： 題型：
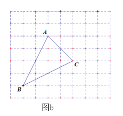
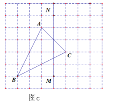
【題目】如圖a,網格中的每一個正方形的邊長為1，△ABC為格點三角形，直線MN為格點直線（點A、B、C、M、N在小正方形的頂點上）.
（1）僅用直尺在圖a中作出△ABC關于直線MN的對稱圖形△A′B′C′.
（2）如圖b，僅用直尺將網格中的格點三角形ABC的面積三等分，并將其中的一份用鉛筆涂成陰影.
（3）如圖c，僅用直尺作三角形ABC的邊AC上的高,簡單說明你的理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
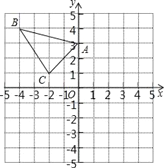
【題目】△ABC在直角坐標系內的位置如圖所示．
（1）分別寫出A、B、C的坐標；
（2）請在這個坐標系內畫出△A1B1C1，使△A1B1C1與△ABC關于y軸對稱，并寫出B1的坐標；
（3）請在這個坐標系內畫出△A2B2C2，使△A2B2C2與△ABC關于原點對稱，并寫出A2的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，將長方形紙片ABCD對折后再展開，得到折痕EF，M是BC上一點，沿著AM再次折疊紙片，使得點B恰好落在折痕EF上的點B′處，連接AB′、BB′．
判斷△AB′B的形狀為 ；
若P為線段EF上一動點，當PB+PM最小時，請描述點P的位置為 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com