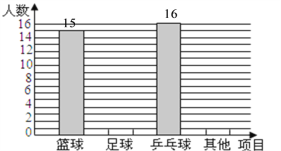
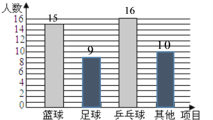
【題目】在大課間活動中，同學們積極參加體育鍛煉，小段同學就本班同學“我最擅長的體育項目”進行了一次調查統計，下面是她通過收集數據后，繪制的兩幅不完整的統計圖．請你根據圖中提供的信息，解答以下問題：
（1）該班共有 名學生；補全條形統計圖；在扇形統計圖中，“其他”部分所對應的圓心角度數為 度.
（2）學校將舉辦冬季運動會，該班已推選5位同學參加乒乓球活動，其中有2位男同學（
、
）和3位女同學（
、
、
），現從中選取兩名同學組成雙打組合，用樹狀圖或列表法求恰好選出一男一女組成混合雙打組合的概率．
【答案】（1）50 72 （2）
【解析】
（1）由籃球項目的人數以及其所占的百分比即可求出該班的人數；由乒乓球項目的人數即可求出，“其它”部分的人數，進而求出“其它”部分所對應的圓心角度數
（2）利用列表法，根據概率公式即可求出恰好選出一男一女組成混合雙打組合的概率
解：（1）該班共有 50 名學生；補全條形統計圖（如圖）；在扇形統計圖中，“其他”部分所對應的圓心角度數為 72 度.
（2）列表：
A | B | C | D | E | |
A | （A，B） | （A，C） | （A，D） | （A，E） | |
B | （B，A） | （B，C） | （B，D） | （B，E） | |
C | （C，A） | （C，B） | （C，D） | （C，E） | |
D | （D，A） | （D，B） | （D，C） | （D，E） | |
E | （E，A） | （E，B） | （E，C） | （E，D） |
一共有20種等可能情況，其中一男一女組成混合雙打組合有12中情況，
（一男一女組成混合雙打組合）
科目：初中數學 來源： 題型：
【題目】已知直線l：y=kx和拋物線C：y=ax2+bx+1．
（1）當k=1，b=1時，拋物線C：y=ax2+bx+1的頂點在直線l：y=kx上，求a的值；
（2）若把直線l向上平移k2+1個單位長度得到直線r，則無論非零實數k取何值，直線r與拋物線C都只有一個交點；
（i）求此拋物線的解析式；
（ii）若P是此拋物線上任一點，過點P作PQ∥y軸且與直線y=2交于點Q，O為原點，
求證：OP=PQ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，BD為△ABC外接圓⊙O的直徑，且∠BAE=∠C．
（1）求證：AE與⊙O相切于點A；
（2）若AE∥BC，BC=2
，AC=2
，求AD的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
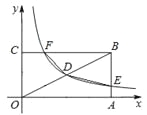
【題目】如圖，矩形OABC的頂點A、C分別在x、y軸的正半軸上，點D為對角線OB的中點，反比例函數
（
）在第一象限內的圖象經過點D，且與AB、BC分別交于E、F兩點，若四邊形BEDF的面積為4.5，則
的值為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，二次函數
的圖象與
軸交于
、
兩點，與
軸交于點
，直線
經過點，與拋物線交于另一點
.已知
，
.
（1）求拋物線與直線的解析式；
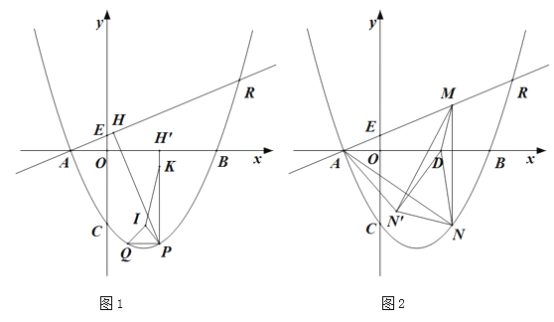
（2）如圖1，若點
是軸下方拋物線上一點，過點作
于點
，過點作
軸交拋物線于點
，過點作
軸于點
，
為直線
上一點，且
.點
為第四象限內一點，且在直線
上方，連接
、
、
.記
，
.當
取得最大值時，求出點的坐標，并求出此時
的最小值.
（3）如圖2，將點沿直線
方向平移13個長度單位到點
，過點作
軸，交拋物線于點
.動點
為軸上一點，連接
、
，再將
沿直線翻折為
（點、、、
在同一平面內），連接
、
、
，當
為等腰三角形時，請直接寫出點的坐標.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在不透明的布袋中裝有1個紅球，2個白球，它們除顏色外其余完全相同．
（1）從袋中任意摸出兩個球，試用樹狀圖或表格列出所有等可能的結果，并求摸出的球恰好是兩個白球的概率；
（2）若在布袋中再添加a個白球，充分攪勻，從中摸出一個球，使摸到紅球的概率為
，試求a的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，在正方形ABCD外取一點E，連接AE、BE、DE．過點A作AE的垂線交DE于點P．若AE=AP=1，PB=
．下列結論：①△APD≌△AEB；②點B到直線AE的距離為
；③EB⊥ED；④S△APD+S△APB=1+
；⑤S正方形ABCD=4+．其中正確結論的序號是（ ）
A.①③④ B．①②⑤ C．③④⑤ D．①③⑤
查看答案和解析>>
科目：初中數學 來源： 題型：
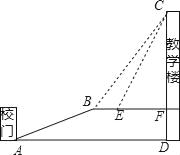
【題目】重慶是一座美麗的山坡，某中學依山而建，校門A處，有一斜坡AB，長度為13米，在坡頂B處看教學樓CF的樓頂C的仰角∠CBF＝53°，離B點4米遠的E處有一花臺，在E處仰望C的仰角∠CEF＝63.4°，CF的延長線交校門處的水平面于D點，FD＝5米．
(1)求斜坡AB的坡度i．
(2)求DC的長．
（參考數據：tan53°≈
，tan63.4°≈2）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
