
【題目】(14分)盤錦紅海灘景區門票價格80元/人,景區為吸引游客,對門票價格進行動態管理,非節假日打a折,節假日期間,10人以下(包括10人)不打折,10人以上超過10人的部分打b折,設游客為x人,門票費用為y元,非節假日門票費用![]() (元)及節假日門票費用
(元)及節假日門票費用![]() (元)與游客x(人)之間的函數關系如圖所示.
(元)與游客x(人)之間的函數關系如圖所示.

(1)a= ,b= ;
(2)直接寫出![]() 、
、![]() 與x之間的函數關系式;
與x之間的函數關系式;
(3)導游小王6月10日(非節假日)帶A旅游團,6月20日(端午節)帶B旅游團到紅海灘景區旅游,兩團共計50人,兩次共付門票費用3040元,求A、B兩個旅游團各多少人?
【答案】(1)6,8;(2)![]() ,
,![]() =
=![]() ;(3)A團有20人,B團有30人.
;(3)A團有20人,B團有30人.
【解析】
試題(1)由函數圖象,用購票款數除以定價的款數,得出a的值;用第11人到20人的購票款數除以定價的款數,得出b的值;
(2)利用待定系數法求正比例函數解析式求出![]() ,分x≤10與x>10,利用待定系數法求一次函數解析式求出
,分x≤10與x>10,利用待定系數法求一次函數解析式求出![]() 與x的函數關系式即可;
與x的函數關系式即可;
(3)設A團有n人,表示出B團的人數為(50﹣n),然后分0≤n≤10與n>10兩種情況,根據(2)的函數關系式列出方程求解即可.
試題解析:(1)由![]() 圖象上點(10,480),得到10人的費用為480元,∴a=
圖象上點(10,480),得到10人的費用為480元,∴a=![]() ×10=6;
×10=6;
由y2圖象上點(10,800)和(20,1440),得到20人中后10人費用為640元,∴b=![]() ×10=8;
×10=8;
(2)設![]() ,∵函數圖象經過點(0,0)和(10,480),∴
,∵函數圖象經過點(0,0)和(10,480),∴![]() ,∴
,∴![]() =48,∴
=48,∴![]() ;
;
0≤x≤10時,設![]() ,∵函數圖象經過點(0,0)和(10,800),∴
,∵函數圖象經過點(0,0)和(10,800),∴![]() ,∴
,∴![]() =80,∴
=80,∴![]() ,x>10時,設
,x>10時,設![]() ,∵函數圖象經過點(10,800)和(20,1440),∴
,∵函數圖象經過點(10,800)和(20,1440),∴![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
∴![]() =
=![]() ;
;
(3)設A團有n人,則B團的人數為(50﹣n),當0≤n≤10時,48n+80(50﹣n)=3040,解得n=30(不符合題意舍去),當n>10時,48n+64(50﹣n)+160=3040,解得n=20,則50﹣n=50﹣20=30.
答:A團有20人,B團有30人.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,點D從點C出發沿CA方向以4cm/秒的速度向點A勻速運動,同時點E從點A出發沿AB方向以2cm/秒的速度向點B勻速運動,當其中一個點到達終點時,另一個點也隨之停止運動.設點D、E運動的時間是t秒(0<t≤15).過點D作DF⊥BC于點F,連接DE,EF.

(1)求證:AE=DF;
(2)四邊形AEFD能夠成為菱形嗎?如果能,求出相應的t值,如果不能,說明理由;
(3)當t為何值時,△DEF為直角三角形?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=BC=4,AO=BO,P是射線CO上的一個動點,∠AOC=60°,則當△PAB為直角三角形時,AP的長為 __________________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與x軸、y軸分別交于點A和點B,點C、D分別為線段AB、OB的中點,點P為OA上一動點,PC+PD值最小時點P的坐標為( )
與x軸、y軸分別交于點A和點B,點C、D分別為線段AB、OB的中點,點P為OA上一動點,PC+PD值最小時點P的坐標為( )

A.(﹣3,0) B.(﹣6,0) C.(![]() ,0) D.(
,0) D.(![]() ,0)
,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知圖①中拋物線y=ax2+bx+c經過點D(﹣1,0)、C(0,﹣1)、E(1,0).
(1)求圖①中拋物線的函數表達式; 
(2)將圖①中拋物線向上平移一個單位,再繞原點O順時針旋轉180°后得到圖②中拋物線,則圖②中拋物線的函數表達式為; 
(3)圖②中拋物線與直線y=﹣ ![]() x﹣
x﹣ ![]() 相交于A、B兩點(點A在點B的左側),如圖③,求點A、B的坐標,并直接寫出當一次函數的值大于二次函數的值時,x的取值范圍.
相交于A、B兩點(點A在點B的左側),如圖③,求點A、B的坐標,并直接寫出當一次函數的值大于二次函數的值時,x的取值范圍. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:一個矩形的兩鄰邊之比為 ![]() ,則稱該矩形為“特比矩形”.
,則稱該矩形為“特比矩形”.
(1)如圖①,在“特比矩形”ABCD中, ![]() =
= ![]() ,求∠AOD的度數;
,求∠AOD的度數; 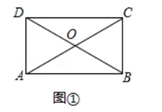
(2)如圖②,特比矩形CDEF的邊CD在半圓O的直徑AB上,頂點E、F在半圓上,已知直徑AB= ![]() ,求矩形CDEF的面積;
,求矩形CDEF的面積; 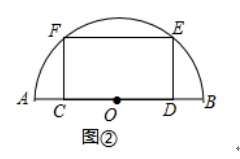
(3)在平面直角坐標系xOy中,⊙O的半徑為 ![]() ,點Q的坐標為(q,2
,點Q的坐標為(q,2 ![]() ),如果在⊙O上存在一點P,過點P作x軸的垂線與過點Q作y軸的垂線交于點M,過點P作y軸的垂線與過點Q作x軸的垂線交于點N,以點P、Q、M、N為頂點的矩形是“特比矩形”,請直接寫出q的取值范圍.
),如果在⊙O上存在一點P,過點P作x軸的垂線與過點Q作y軸的垂線交于點M,過點P作y軸的垂線與過點Q作x軸的垂線交于點N,以點P、Q、M、N為頂點的矩形是“特比矩形”,請直接寫出q的取值范圍. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校實施課程改革,為初三學生設置了A,B,C,D,E,F共六門不同的拓展性課程,現隨機抽取若干學生進行了“我最想選的一門課”調查,并將調查結果繪制成如圖統計圖表(不完整)
選修課 | A | B | C | D | E | F |
人數 | 20 | 30 |
根據圖標提供的信息,下列結論錯誤的是( )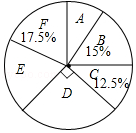
A.這次被調查的學生人數為200人
B.扇形統計圖中E部分扇形的圓心角為72°
C.被調查的學生中最想選F的人數為35人
D.被調查的學生中最想選D的有55人
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明在學習過程中遇到這樣一個問題:
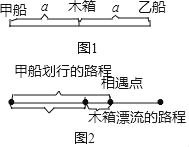
“一個木箱漂浮在河水中,隨河水向下游漂去,在木箱上游和木箱下游各有一條小船,分別為甲船和乙船,兩船距木箱距離相等,同時劃向木箱,若兩船在靜水中劃行的速度是30m/min,那么哪條小船先遇到木箱?”
小明是這樣分析解決的:
小明想通過比較甲乙兩船遇見木箱的時間,知道哪條小船先遇見木箱.設甲船遇見木箱的時間為xmin,乙船遇見木箱的時間為ymin,開始時兩船與木箱距離相等,都設為am,如圖1.
如圖2,利用甲船劃行的路程﹣木箱漂流的路程=開始時甲船與木箱的距離:
列方程:x(30+5)﹣5x=a
解得,x=![]()
所以甲船遇見木箱的時間為![]() min.
min.
(1)參照小明的解題思路繼續完成上述問題;
(2)借鑒小明解決問題的方法和(1)中發現的結論解決下面問題:
問題:“在一河流中甲乙兩條小船,同時從A地出發,甲船逆流而上,乙船順流而下;劃行10分鐘后,乙船發現船上木箱不知何時掉入水中,乙船立即通知甲船,兩船同時掉頭尋找木箱,若兩船在靜水中劃行的速度是v(單位:m/min,v大于5),水流速度是5m/min,兩船同時遇見木箱,那么木箱是出發幾分鐘后掉入水中的?”
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com