
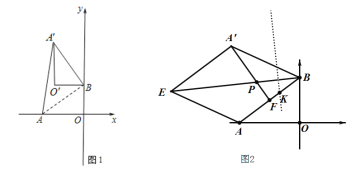
【題目】在平面直角坐標(biāo)系中,O為原點(diǎn),點(diǎn)A(4,0),點(diǎn)B(0,3),△ABO繞點(diǎn)B順時(shí)針旋轉(zhuǎn),得△A′BO′,點(diǎn)A、O旋轉(zhuǎn)后的對應(yīng)點(diǎn)為A′、O′,記旋轉(zhuǎn)角為α.
(1)如圖1,若α=90°,求AA′的長;
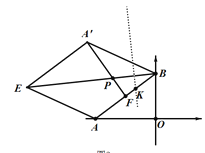
(2)在(1)的條件下,邊OA上的一點(diǎn)M旋轉(zhuǎn)后的對應(yīng)點(diǎn)為N,當(dāng)O′M+BN取得最小值時(shí),在圖中畫出求點(diǎn)M的位置,并求出點(diǎn)N的坐標(biāo)。
(3)如圖2,在△ABO繞點(diǎn)B順時(shí)針旋轉(zhuǎn)過程中,以AB、A′B為鄰邊畫菱形AB A′E,F是AB的中點(diǎn),連A′F交BE于P,BP的垂直平分線交AB于K,當(dāng)α從60°到90°的變化過程中,點(diǎn)K的位置是否變化?若不變,求BK的長并直接寫出此變化過程中點(diǎn)P的運(yùn)動(dòng)路徑長.
【答案】(1)AA'=![]() ;(2)作圖見解析,N(﹣3,
;(2)作圖見解析,N(﹣3,![]() );(3)不發(fā)生變化,
);(3)不發(fā)生變化,![]()
【解析】
(1)先求出AB的長度,然后利用旋轉(zhuǎn)的性質(zhì)得到![]() ,然后得到
,然后得到![]() 的長度;
的長度;
(2)根據(jù)題意,利用軸對稱的性質(zhì),先確定出點(diǎn)M的位置,然后求出點(diǎn)M的坐標(biāo),利用旋轉(zhuǎn)的性質(zhì),即可得到點(diǎn)N的坐標(biāo);
(3)根據(jù)菱形的性質(zhì),得到△FBP∽△A′EP,然后結(jié)合相似三角形的性質(zhì)和平行線分線段成比例,求出BK的長度;根據(jù)弧長公式,即可求出點(diǎn)P的運(yùn)動(dòng)路徑長.
解:(1)∵A(﹣4,0),點(diǎn)B(0,3),
∴OA=4,OB=3
由勾股定理得:AB=![]() ,
,
∵旋轉(zhuǎn)角![]() =90°,
=90°,
由旋轉(zhuǎn)知A'B=AB=5,
∴△A'BA是等腰直角三角形,
∴AA'=![]() ;
;
(2)由旋轉(zhuǎn)知BN=BM,
∴O′M+BN的最小值=O′M+BM的最小值,
∴作出點(diǎn)B(0,3)關(guān)于x軸的對稱點(diǎn)B'(0,﹣3),連接O'B'交OA于點(diǎn)M,點(diǎn)M即為所求;
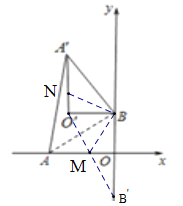
設(shè)O′B':y=kx+b把O′(﹣3,3)B'(0,﹣3)代入得
![]() ,
,
解得:k=﹣2,b=﹣3,
∴O′B'為y=﹣2x﹣3;
令'y=0得:x=﹣![]() ,
,
∴M(﹣![]() ,0),MO =
,0),MO =![]() ,
,
∵由旋轉(zhuǎn)的性質(zhì)得△BOM≌△BO′N,
∴OM =O′N=![]() ,
,
∴N的縱坐標(biāo)為:3+![]() =
=![]() ,
,
∴N(﹣3,![]() );
);
(3)不發(fā)生變化;理由如下:
∵F是BC的中點(diǎn),
∴BF=AF=![]() AB,
AB,
∵四邊形AB A′E是菱形,
∴AB=A′E,AB∥A′E,
∴△FBP∽△A′EP,
∴![]() ,
,
∵四邊形AB A′E是菱形,
∴∠ABE=∠A′ BE,
又∵BP的中垂線與邊AB交于點(diǎn)K,
∴KP=KB,
∴∠ABE=∠KPB,
∴∠KPB=∠A′ BE,
∴PK∥AE∥A′ B,
∴![]() ,
,
∴BK=![]() AB=
AB=![]() ,
,
即點(diǎn)K的位置不發(fā)生改變;
∴P點(diǎn)經(jīng)過路線是以K為圓心,BK為半徑的圓弧,
長度為: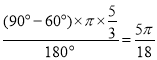 .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位線,點(diǎn)M是邊BC上一點(diǎn),BM=3,點(diǎn)N是線段MC上的一個(gè)動(dòng)點(diǎn),連接DN,ME,DN與ME相交于點(diǎn)O.若△OMN是直角三角形,則DO的長是______.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】當(dāng)今社會人們越來越離不開網(wǎng)絡(luò),電腦、手機(jī)被普遍使用,與此同時(shí)人們的視力也大大受到影響,2019年初某企業(yè)以25萬元購得某項(xiàng)護(hù)目鏡生產(chǎn)技術(shù)后,再投人100萬元購買生產(chǎn)設(shè)備,進(jìn)行該護(hù)目鏡的生產(chǎn)加工,已知生產(chǎn)這種護(hù)目鏡的成本價(jià)為每件20元,經(jīng)過市場調(diào)研發(fā)現(xiàn)該產(chǎn)品的銷售單價(jià)定在![]() 元比較合理,并且該產(chǎn)品的年銷售量
元比較合理,并且該產(chǎn)品的年銷售量![]() (萬件)與銷售單價(jià)
(萬件)與銷售單價(jià)![]() (元)之間的函數(shù)關(guān)系式為
(元)之間的函數(shù)關(guān)系式為![]() .(年獲利=年銷售收入-生產(chǎn)成本-投資成本)
.(年獲利=年銷售收入-生產(chǎn)成本-投資成本)
(1)求該公司第一年的年獲利![]() (萬元)與銷售單價(jià)
(萬元)與銷售單價(jià)![]() (元)之間的函數(shù)關(guān)系式,并說明投資的第一年,該公司是盈利還是虧損?若盈利,最大利潤是多少?若虧損,最小虧損是多少?
(元)之間的函數(shù)關(guān)系式,并說明投資的第一年,該公司是盈利還是虧損?若盈利,最大利潤是多少?若虧損,最小虧損是多少?
(2)2020年初我國爆發(fā)新冠肺炎,該公司決定向紅十字會捐款20萬元,另外每銷售一件產(chǎn)品,就抽出1元錢作為捐款,若除去第一年的最大盈利(或最小虧損)以及第二年的捐款后,到2020年底,兩年的總盈利不低于57.5萬元,請你確定此時(shí)銷售單價(jià)的范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】定義:我們把關(guān)于某一點(diǎn)成中心對稱的兩條拋物線叫“孿生拋物線”;(1)已知拋物線L:y=﹣x2+4與x軸交于A、B兩點(diǎn)(A在B的左側(cè)),與y軸交于C點(diǎn),求L關(guān)于坐標(biāo)原點(diǎn)O(0,0)的“孿生拋物線”W;(2)點(diǎn)N為坐標(biāo)平面內(nèi)一點(diǎn),且△BCN是以BC為斜邊的等腰直角三角形,在x軸是否存在一點(diǎn)M(m,0),使拋物線L關(guān)于點(diǎn)M的“孿生拋物線”過點(diǎn)N,如果存在,求出M點(diǎn)坐標(biāo);不存在,說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩所醫(yī)院分別有一男一女共4名醫(yī)護(hù)人員支援湖北武漢抗擊疫情.
(1)若從甲、乙兩醫(yī)院支援的醫(yī)護(hù)人員中分別隨機(jī)選1名,則所選的2名醫(yī)護(hù)人員性別相同的概率是 ;
(2)若從支援的4名醫(yī)護(hù)人員中隨機(jī)選2名,用列表或畫樹狀圖的方法求出這2名醫(yī)護(hù)人員來自同一所醫(yī)院的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為落實(shí)“綠水青山就是金山銀山”的發(fā)展理念,某市政部門招標(biāo)一工程隊(duì)負(fù)責(zé)在山腳下修建一座水庫的土方施工任務(wù).該工程隊(duì)有![]() 兩種型號的挖掘機(jī),已知3臺
兩種型號的挖掘機(jī),已知3臺![]() 型和5臺
型和5臺![]() 型挖掘機(jī)同時(shí)施工一小時(shí)挖土165立方米;4臺
型挖掘機(jī)同時(shí)施工一小時(shí)挖土165立方米;4臺![]() 型和7臺
型和7臺![]() 型挖掘機(jī)同時(shí)施工一小時(shí)挖土225立方米.每臺
型挖掘機(jī)同時(shí)施工一小時(shí)挖土225立方米.每臺![]() 型挖掘機(jī)一小時(shí)的施工費(fèi)用為300元,每臺
型挖掘機(jī)一小時(shí)的施工費(fèi)用為300元,每臺![]() 型挖掘機(jī)一小時(shí)的施工費(fèi)用為180元.
型挖掘機(jī)一小時(shí)的施工費(fèi)用為180元.
(1)分別求每臺![]() 型,
型, ![]() 型挖掘機(jī)一小時(shí)挖土多少立方米?
型挖掘機(jī)一小時(shí)挖土多少立方米?
(2)若不同數(shù)量的![]() 型和
型和![]() 型挖掘機(jī)共12臺同時(shí)施工4小時(shí),至少完成1080立方米的挖土量,且總費(fèi)用不超過12960元.問施工時(shí)有哪幾種調(diào)配方案,并指出哪種調(diào)配方案的施工費(fèi)用最低,最低費(fèi)用是多少元?
型挖掘機(jī)共12臺同時(shí)施工4小時(shí),至少完成1080立方米的挖土量,且總費(fèi)用不超過12960元.問施工時(shí)有哪幾種調(diào)配方案,并指出哪種調(diào)配方案的施工費(fèi)用最低,最低費(fèi)用是多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知直線![]() 與⊙
與⊙![]() 相離.
相離.![]() 于點(diǎn)
于點(diǎn)![]() ,交⊙
,交⊙![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() ,
,![]() 與⊙
與⊙![]() 相切于點(diǎn)
相切于點(diǎn)![]() ,
,![]() 的延長線交直線
的延長線交直線![]() 于點(diǎn)
于點(diǎn)![]() .
.
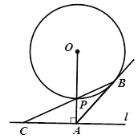
(1)求證:![]() ;
;
(2)若![]() ,求⊙
,求⊙![]() 的半徑.
的半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】拋物線![]() 的對稱軸為直線
的對稱軸為直線![]() .若關(guān)于
.若關(guān)于![]() 的一元二次方程
的一元二次方程![]() 在
在![]() 的范圍內(nèi)有實(shí)數(shù)根,則
的范圍內(nèi)有實(shí)數(shù)根,則![]() 的取值范圍是_____________.
的取值范圍是_____________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】春節(jié)期間,某商場計(jì)劃購進(jìn)甲、乙兩種商品,已知購進(jìn)甲商品2件和乙商品3件共需270元;購進(jìn)甲商品3件和乙商品2件共需230元.
(1)求甲、乙兩種商品每件的進(jìn)價(jià)分別是多少元?
(2)商場決定甲商品以每件40元出售,乙商品以每件90元出售,為滿足市場需求,需購進(jìn)甲、乙兩種商品共100件,且甲種商品的數(shù)量不少于乙種商品數(shù)量的4倍,請你求出獲利最大的進(jìn)貨方案,并確定最大利潤.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com