【題目】在等腰Rt△ABC中，D為斜邊AB的中點，點E在AC上，且∠EDC=72°，點F在AB上，滿足DE=DF，則∠CEF的度數為_______.
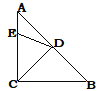
【答案】54°或144°
【解析】分析：分兩種情況：①點F在AD上時，可求出∠DEF=81°，在△CDE中可求出∠CED=63°，故可求出∠CEF=144°；②點F在DB上時，可求出∠DEF=9°,故可求出∠CEF=54°.
詳解：①點F在AD上時，如圖1，
∵AC=BC,D是AB的中點，且∠ACB=90°,
∴∠ADC=90°，∠DCE=45°
∵∠CDE=72°
∴∠EDF=18°
∵DE=DF
∴∠DEF=81°
在△ECD中，∠CDE=72°,∠ECD=45°
∴∠CED=63°，
∴∠CEF=144°；
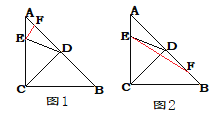
②點F在DB上時，如圖2.
同理得，∠DEF=9°,
∴∠CEF=54°.
故答案為：54°或144°.
科目：初中數學 來源： 題型：
【題目】如圖，將兩塊完全相同的矩形紙片ABCD和矩形紙片AEFG按圖示方式放置（點A、D、E在同一直線上），連接AC、AF、CF，已知AD＝3，DC＝4，則CF的長是（ ）
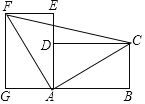
A.5B.7C.5
D.10
查看答案和解析>>
科目：初中數學 來源： 題型：
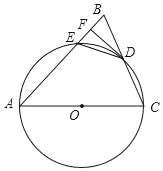
【題目】如圖，在△ABC中，AB=AC，以AC為直徑的⊙O交BC于點D，交AB于點E，過點D作DF⊥AB，垂足為F，連接DE．
（1）求證：直線DF與⊙O相切；
（2）求證：BF=EF；
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，小明想利用太陽光測量樓高，發現對面墻上有這棟樓的影子，小明邊移動邊觀察，發現站到點E處時，可以使自己落在墻上的影子與這棟樓落在墻上的影子重疊且高度恰好相同．此時測得墻上影子高
，
，
（點A、E、C在同一直線上）．已知小明身高EF是1.6m，則樓高AB為______m．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某報社為了解市民對“社會主義核心價值觀”的知曉程度，采取隨機抽樣的方式進行問卷調查，調查結果分為“A．非常了解”、“B．了解”、“C．基本了解”三個等級，并根據調查結果繪制了如下兩幅不完整的統計圖．
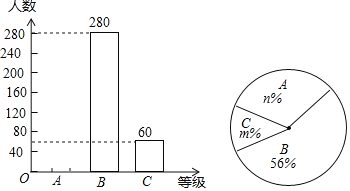
（1）這次調查的市民人數為_____人；
（2）補全條形統計圖；
（3）計算扇形統計圖中等級C對應的圓心角的度數；
（4）若該市約有市民1000000人，請你根據抽樣調查的結果，估計該市大約有多少人對“社會主義核心價值觀”達到“A．非常了解”的程度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為積極響應“弘揚傳統文化”的號召，某學校倡導全校1200名學生進行經典詩詞誦背活動，并在活動之后舉辦經典詩詞大賽，為了解本次系列活動的持續效果，學校團委在活動啟動之初，隨機抽取部分學生調查“一周詩詞誦背數量”，根據調查結果繪制成的統計圖(部分)如下圖所示：
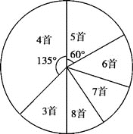
大賽結束后一個月，再次調查這部分學生“一周詩詞誦背數量”，繪制成統計表：
一周詩詞誦背數量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人 數 | 10 | 10 | 15 | m | 25 | 20 |
請根據調查的信息
(1)本次調查抽取了多少名學生？
(2)補全條形統計圖，在扇形統計圖中，“6首”的圓心角為 度；
(3)表格中m的值為 ；
(4)估計大賽后一個月該校學生一周詩詞誦背6首(含6首)以上的人數；
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在二次函數y＝ax2+bx+c的圖象中，你認為其中正確的是（ ）
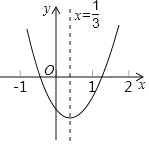
A. a＞0 B. c＞0
C. b2﹣4ac＜0 D. 一元二次方程ax2+bx+c＝0有兩個相等實根
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有甲、乙兩名采購員去同一家公司分別購買兩次飼料，兩次購買的飼料價格分別為m元/千克和n元/千克，且m≠n，兩名采購員的采購方式也不同，其中甲每次購買800千克，乙每次用去800元，而不管購買多少千克的飼料。
（1）甲、乙兩次購買飼料的平均單價各是多少？（用字母m、n表示）
（2）誰的購買方式比較合算?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
