
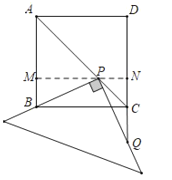
【題目】如圖,將一個三角板放在邊長為1的正方形![]() 上,并使它的直角頂點
上,并使它的直角頂點![]() 在對角線
在對角線![]() 上滑動,直角的一邊始終經過點
上滑動,直角的一邊始終經過點![]() ,另一邊與射線
,另一邊與射線![]() 相交于點
相交于點![]() .
.

(1)當點![]() 在
在![]() 邊上時,過點
邊上時,過點![]() 作
作![]() 分別交
分別交![]() ,
,![]() 于點
于點![]() ,
,![]() ,證明:
,證明:![]() ;
;
(2)當點![]() 在線段
在線段![]() 的延長線上時,設
的延長線上時,設![]() 、
、![]() 兩點間的距離為
兩點間的距離為![]() ,
,![]() 的長為
的長為![]() .
.
①直接寫出![]() 與
與![]() 之間的函數關系,并寫出函數自變量
之間的函數關系,并寫出函數自變量![]() 的取值范圍;
的取值范圍;
②![]() 能否為等腰三角形?如果能,直接寫出相應的
能否為等腰三角形?如果能,直接寫出相應的![]() 值;如果不能,說明理由.
值;如果不能,說明理由.
【答案】(1)見解析;(2)① .②
.②![]() 能為等腰三角形,
能為等腰三角形,![]() .
.
【解析】
(1)根據正方形的性質證明![]() ,即可求解;
,即可求解;
(2)①根據題意作圖,由正方形的性質可知當![]() 時,點
時,點![]() 在線段
在線段![]() 的延長線上,同理可得
的延長線上,同理可得![]() ,得到MP=NQ,利用等腰直角三角形的性質可知MP=
,得到MP=NQ,利用等腰直角三角形的性質可知MP=![]() x,NC=CD-DN=1-
x,NC=CD-DN=1-![]() x,CQ=y,代入MP=NQ化簡即可求解;
x,CQ=y,代入MP=NQ化簡即可求解;
②由![]() 是等腰三角形,∠PCQ=135°,CP=CQ成立,代入解方程即可求解 ,
是等腰三角形,∠PCQ=135°,CP=CQ成立,代入解方程即可求解 ,
(1)證明:∵在正方形![]() 中,
中,![]() 為對角線,
為對角線,
∴![]() ,
,![]() ,∵
,∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
又∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,
∵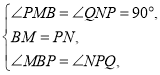
∴![]() ,∴
,∴![]() .
.
(2)①如圖,點![]() 在線段
在線段![]() 的延長線上,
的延長線上,
同(1)可證![]() ,
,
∴MP=NQ,
在等腰直角三角形AMP中,AP=![]() =x
=x
∴MP=![]() x=AM,
x=AM,
∴NC=BM=AB-AM=1-![]() x
x
故NQ=NC+CQ=1-![]() x+y
x+y
∴![]() x=1-
x=1-![]() x+y
x+y
化簡得![]()
當P點位于AC中點時,Q點恰好在C點,又AP<AC=![]()
∴![]()
∴![]() 與
與![]() 之間的函數關系是
之間的函數關系是![]() (
(![]() )
)
②當![]() 時,
時,![]() 能為等腰三角形,
能為等腰三角形,
理由:當點![]() 在
在![]() 的延長線上,CQ=
的延長線上,CQ=![]() ,CQ=AC-AP=
,CQ=AC-AP=![]() ,
,
由![]() 是等腰三角形,∠PCQ=∠PCB+∠BCQ=45°+90°=135°,
是等腰三角形,∠PCQ=∠PCB+∠BCQ=45°+90°=135°,
∴CP=CQ成立,
即![]() 時,解得
時,解得![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,把一個木制正方體的表面涂上顏色,然后將正方形分割成27個大小相同的小正方體,從這些小正方體中任意取出一個,求取出的小正方體;
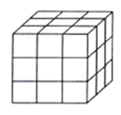
(1)只有一面涂有顏色的概率;
(2)至少有兩面涂有顏色的概率;
(3)各個面都沒有顏色的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了響應市委和市政府“綠色環保,節能減排”的號召,幸福商場用3300元購進甲、乙兩種節能燈共計100只,很快售完.這兩種節能燈的進價、售價如下表:
進價(元/只) | 售價(元/只) | |
甲種節能燈 | 30 | 40 |
甲種節能燈 | 35 | 50 |
(1)求幸福商場甲、乙兩種節能燈各購進了多少只?
(2)全部售完100只節能燈后,商場共計獲利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學興趣小組活動中,小明進行數學探究活動,將邊長為![]() 的正方形ABCD與邊長為
的正方形ABCD與邊長為![]() 的正方形AEFG按圖1位置放置,AD與AE在同一條直線上,AB與AG在同一條直線上.
的正方形AEFG按圖1位置放置,AD與AE在同一條直線上,AB與AG在同一條直線上.
(1)小明發現DG⊥BE,請你幫他說明理由.
(2)如圖2,小明將正方形ABCD繞點A逆時針旋轉,當點B恰好落在線段DG上時,請你幫他求出此時BE的長.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】暑假期間,兩位家長計劃帶領若干名學生去旅游,他們聯系了報價均為每人1000元的兩家旅行社.經協商,甲旅行社的優惠條件是:兩位家長全額收費,學生都按7折收費;乙旅行社的優惠條件是:學生、家長都按8折收費.假設這兩位家長帶領x名學生去旅行,甲、乙旅行社的收費分別為y甲,y乙,
(1)寫出y甲,y乙與x的函數關系式.
(2)學生人數在什么情況下,選擇哪個旅行社合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() ,
,![]() ,求
,求![]() 的度數.
的度數.

(1)填空,在空白處填上結果或者理由.
解:過點![]() 作
作![]() ,(如圖)
,(如圖)
得![]() ___________°, ( )
___________°, ( )
又因為![]() ,(已知)
,(已知)
所以![]() ___________°.
___________°.
因為![]() ,
,
所以![]() , ( )
, ( )
又因為![]() ,(已知)
,(已知)
所以![]() ___________°,
___________°,
所以![]() ___________°.
___________°.
(2)請用另一種解法求![]() 的度數.
的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
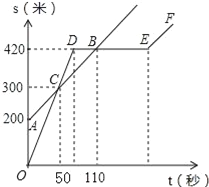
【題目】某中學的小明和朱老師一起到一條筆直的跑道上鍛煉身體,到達起點后小明做了一會準備活動朱老師先跑,當小明出發時,朱老師已經距起點200米了,他們距起點的距離s(米)與小明出發的時間t(秒)之間的關系如圖所示(不完整).根據圖中給出的信息,解答下列問題:
(1)在上述變化過程中,自變量是 ,因變量是 ;
(2)朱老師的速度為 米/秒;小明的速度為 米/秒;
(3)小明與朱老師相遇 次,相遇時距起點的距離分別為 米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】當行駛中的汽車撞到物體時,汽車的損壞程度通常用“撞擊影響”來衡量.汽車的撞擊影響I可以用汽車行駛速度v(km/min)來表示,下表是某種型號汽車的行駛速度與撞擊影響的試驗數據:
v(km/min) | 0 | 1 | 2 | 3 | 4 |
I | 0 | 2 | 8 | 18 | 32 |
(1)請根據上表中的數據,在直角坐標系中描出坐標(v,I)所對應的點,并用光滑曲線將各點連接起來;

(2)填寫下表,并根據表中數據的呈現規律,猜想用v表示I的二次函數表達式;
v(km/min) | 1 | 2 | 3 | 4 |
|
|
|
|
|
(3)當汽車的速度分別是1.5 km/min,2.5 km/min,4.5 km/min時,利用你得到的撞擊影響公式,計算撞擊影響分別是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,MN∥OP,點A為直線MN上一定點,B為直線OP上的動點,在直線MN與OP之間且在線段AB的右方作點D,使得AD⊥BD.設∠DAB=α(α為銳角).
(1)求∠NAD與∠PBD的和;(提示過點D作EF∥MN)
(2)當點B在直線OP上運動時,試說明∠OBD﹣∠NAD=90°;
(3)當點B在直線OP上運動的過程中,若AD平分∠NAB,AB也恰好平分∠OBD,請求出此時α的值

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com