
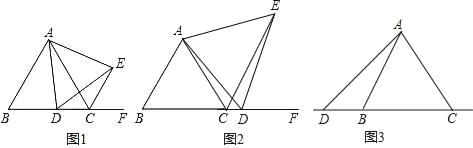
【題目】已知△ABC為等邊三角形,點D為直線BC上的一動點(點D不與B、C重合),以AD為邊作等邊△ADE(頂點A、D、E按逆時針方向排列),連接CE.
(1)如圖1,當點D在邊BC上時,求證:①BD=CE,②AC=CE+CD;
(2)如圖2,當點D在邊BC的延長線上且其他條件不變時,結論AC=CE+CD是否成立?若不成立,請寫出AC、CE、CD之間存在的數量關系,并說明理由;
(3)如圖3,當點D在邊BC的反向延長線上且其他條件不變時,補全圖形,并直接寫出AC、CE、CD之間存在的數量關系.
【答案】(1)①證明見解析;②證明見解析;(2)AC=CE+CD不成立,AC、CE、CD之間存在的數量關系是:AC=CE﹣CD,理由見解析;(3)補圖見解析;AC=CD﹣CE.
【解析】
(1)根據等邊三角形的性質及等式的性質證明△ABD≌△ACE,從而得出結論;
(2)根據等邊三角形的性質及等式的性質就可以得出△ABD≌△ACE,就可以得出BD=CE,就可以得出AC=CE﹣CD;
(3)先根據條件畫出圖形,根據等邊三角形的性質及等式的性質就可以得出△ABD≌△ACE,就可以得出BD=CE,就可以得出AC=CD﹣CE.
(1)∵△ABC和△ADE都是等邊三角形,
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°.
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,即∠BAD=∠CAE.
在△ABD和△ACE中,
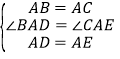 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE.
∵BC=BD+CD,AC=BC,
∴AC=CE+CD;
(2)AC=CE+CD不成立,
AC、CE、CD之間存在的數量關系是:AC=CE﹣CD.
理由:∵△ABC和△ADE都是等邊三角形,
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°.
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE
在△ABD和△ACE中,
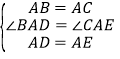
∴△ABD≌△ACE(SAS)
∴BD=CE
∴CE﹣CD=BD﹣CD=BC=AC,
∴AC=CE﹣CD;
(3)補全圖形(如圖)
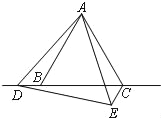
AC、CE、CD之間存在的數量關系是:AC=CD﹣CE.
理由:∵△ABC和△ADE都是等邊三角形,
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°.
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,
∴∠BAD=∠CAE
在△ABD和△ACE中,
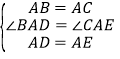
∴△ABD≌△ACE(SAS)
∴BD=CE.
∵BC=CD﹣BD,
∴BC=CD﹣CE,
∴AC=CD﹣CE.


科目:初中數學 來源: 題型:
【題目】某校八年級640名學生在“計算機應用”培訓前、后各參加了一次水平相同的測試,并以同一標準分成“不合格”、“合格”、“優秀”3個等級,為了解培訓效果,用抽樣調查的方式從中抽取32名學生的2次測試等級,并繪制成條形統計圖:

(1)這32名學生經過培訓,測試等級“不合格”的百分比比培訓前減少了多少?
(2)估計該校八年級學生中,培訓前、后等級為“合格”與“優秀”的學生各有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
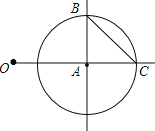
【題目】如圖, ![]() ,以點A為圓心,1為半徑畫
,以點A為圓心,1為半徑畫![]() 與OA的延長線交于點C,過點A畫OA的垂線,垂線與
與OA的延長線交于點C,過點A畫OA的垂線,垂線與![]() 的一個交點為B,連接BC
的一個交點為B,連接BC
![]() 線段BC的長等于______;
線段BC的長等于______;
![]() 請在圖中按下列要求逐一操作,并回答問題:
請在圖中按下列要求逐一操作,并回答問題:
![]() 以點______為圓心,以線段______的長為半徑畫弧,與射線BA交于點D,使線段OD的長等于
以點______為圓心,以線段______的長為半徑畫弧,與射線BA交于點D,使線段OD的長等于![]()
![]() 連OD,在OD上畫出點P,使OP的長等于
連OD,在OD上畫出點P,使OP的長等于![]() ,請寫出畫法,并說明理由.
,請寫出畫法,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】節約用水是我們的美德,水龍頭關閉不嚴會造成滴水,容器內盛水![]() 與滴水時間
與滴水時間![]() 的關系用可以顯示水量的容器做如圖
的關系用可以顯示水量的容器做如圖![]() 的試驗,并根據試驗數據繪制出如圖
的試驗,并根據試驗數據繪制出如圖![]() 的函數圖象,結合圖象解答下列問題.
的函數圖象,結合圖象解答下列問題.
(![]() )容器內原有水多少升.
)容器內原有水多少升.
(![]() )求
)求![]() 與
與![]() 之間的函數關系式,并計算在這種滴水狀態下一天的滴水量是多少升.
之間的函數關系式,并計算在這種滴水狀態下一天的滴水量是多少升.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是等腰直角三角形
是等腰直角三角形![]() 底邊
底邊![]() 上的高,點
上的高,點![]() 是
是![]() 的中點,延長
的中點,延長![]() 到
到![]() ,使
,使![]() ,連接
,連接![]() .
.
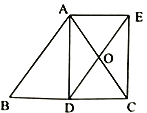
(1)求證:四邊形![]() 是矩形;
是矩形;
(2)填空:
①若![]() ,
,![]() ,則四邊形
,則四邊形![]() 的面積=_____:
的面積=_____:
②若![]() ,則
,則![]() ____時,四邊形
____時,四邊形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小亮參加中華詩詞大賽,還剩最后兩題,如果都答對,就可順利通關.其中第一道單選題有4個選項,第二道單選題有3個選項.小亮這兩道題都不會,不過還有一個“求助”沒有使用(使用求助可以讓主持人去掉其中一題的一個錯誤選項).
(1)如果小亮第一題使用“求助”,那么他答對第一道題的概率是__;
(2)他的親友團建議:最后一題使用“求助”,從提高通關的可能性的角度看,你同意親友團的觀點嗎?試說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知數軸上三點M,O,N對應的數分別為-3,0,1,點P為數軸上任意一點,其對應的數為x.
(1)如果點P到點M,點N的距離相等,那么x的值是______________;
(2)數軸上是否存在點P,使點P到點M,點N的距離之和是5?若存在,請直接寫出x的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com