
【題目】小亮和小瑩自制了一個標靶進行投標比賽,兩人各投了10次,如圖是他們投標成績的統計圖.
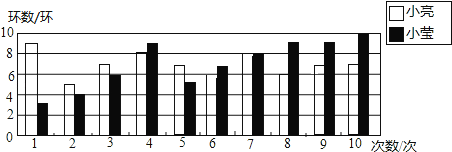
(1)根據圖中信息填寫下表
平均數 | 中位數 | 眾數 | |
小亮 | 7 | ||
小瑩 | 7 | 9 |
(2)分別用平均數和中位數解釋誰的成績比較好.
【答案】解:(1)填表如下:
平均數 | 中位數 | 眾數 | |
小亮 | 7 | 7 | 7 |
小瑩 | 7 | 7.5 | 9 |
(2)平均數相等說明:兩人整體水平相當,成績一樣好;
小瑩的中位數大說明:小瑩的成績比小亮好。
【解析】
試題分析:(1)根據條形統計圖找出小亮與小瑩10次投中的環數,求出平均數,中位數,以及眾數即可:
根據題意得:小亮的環數為:9,5,7,8,7,6,8,6,7,7,
平均數為![]() (9+5+7+8+7+6+8+6+7+7)=7(環),中位數為7,眾數為7;
(9+5+7+8+7+6+8+6+7+7)=7(環),中位數為7,眾數為7;
小瑩的環數為:3,4,6,9,5,7,8,9,9,10,
平均數為![]() (3+4+6+9+5+7+8+9+9+10)=7(環),中位數為7.5,眾數為9。
(3+4+6+9+5+7+8+9+9+10)=7(環),中位數為7.5,眾數為9。
(2)根據兩人的中位數相同,可得出誰的平均數高,誰的成績好。


科目:初中數學 來源: 題型:
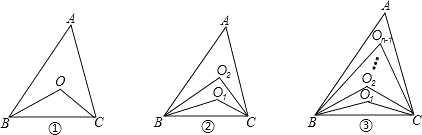
【題目】已知△ABC中,∠A=50°.
(1)如圖①,∠ABC、∠ACB的角平分線交于點O,則∠BOC= °.
(2)如圖②,∠ABC、∠ACB的三等分線分別對應交于O1、O2,則∠BO2C= °.
(3)如圖③,∠ABC、∠ACB的n等分線分別對應交于O1、O2…On﹣1(內部有n﹣1個點),求∠BOn﹣1C(用n的代數式表示).
(4)如圖③,已知∠ABC、∠ACB的n等分線分別對應交于O1、O2…On﹣1,若∠BOn﹣1C=60°,求n的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一組數據中,隨機抽取50個作為樣本進行統計,在頻數分布表中,54.5~57.5這一組的頻率是0.12,那么這個樣本中的數據落在54.5~57.5之間的有__個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探索發現:
如圖1,已知直線l1∥l2 , 且l3和l1、l2分別相交于A、B兩點,l4和l1、l2分別交于C、D兩點,∠ACP記作∠1,∠BDP記作∠2,∠CPD記作∠3.點P在線段AB上.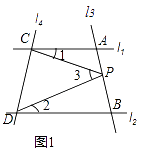
(1)若∠1=20°,∠2=30°,請你求出∠3的度數.
(2)請你根據上述問題,請你找出圖1中∠1、∠2、∠3之間的數量關系,并直接寫出你的結論.
(3)應用(2)中的結論解答下列問題:如圖2,點A在B的北偏東 40°的方向上,在C的北偏西45°的方向上,請你根據上述結論直接寫出∠BAC的度數.
拓展延伸:
(4)如果點P在直線l3上且在A、B兩點外側運動時,其他條件不變,試探究∠1、∠2、∠3之間的關系(點P和A、B兩點不重合),寫出你的結論并說明理由.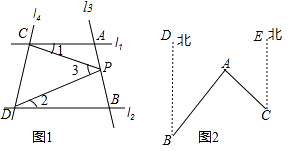
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人在相同條件下各射靶10次,每次射靶的成績情況如圖所示:
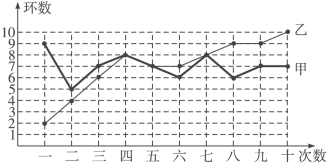
(1)請填寫下表:
平均數 | 方差 | 中位數 | 命中9環及以上的次數 | |
甲 | 7 | 1.2 | 1 | |
乙 | 5.4 |
(2)請從下列四個不同的角度對這次測試結果進行分析:
①從平均數和方差相結合看;
②從平均數和中位數相結合看(分析誰的成績好些);
③從平均數和命中9環以上的次數相結合看(分析誰的成績好些);
④從折線圖上兩人射擊命中環數的走勢看(分析誰更有潛力).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“龜兔賽跑”講述了這樣的故事:領先的兔子看著緩慢爬行的烏龜,驕傲起來,睡了一覺,當它醒來時,發現烏龜快到終點了,于是急忙追趕,但為時已晚,烏龜還是先到達終點、用s1、s2分別表示烏龜和兔子所行的路程,t為時間,則下列圖象中與故事情節相吻合的是( )
A.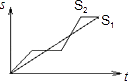
B.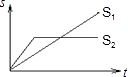
C.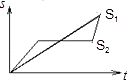
D.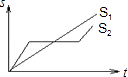
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線CB∥OA,∠C=∠OAB=100°,E、F在CB上,且滿足∠FOB=∠AOB,OE平分∠COF 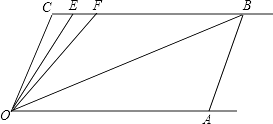
(1)求∠EOB的度數;
(2)若平行移動AB,那么∠OBC:∠OFC的值是否隨之發生變化?若變化,找出變化規律或求出變化范圍;若不變,求出這個比值
(3)在平行移動AB的過程中,是否存在某種情況,使∠OEC=∠OBA?若存在,求出其度數;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com