
【題目】已知△ABC中,∠A=50°.
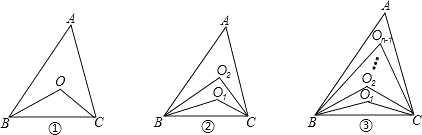
(1)如圖①,∠ABC、∠ACB的角平分線交于點O,則∠BOC= °.
(2)如圖②,∠ABC、∠ACB的三等分線分別對應交于O1、O2,則∠BO2C= °.
(3)如圖③,∠ABC、∠ACB的n等分線分別對應交于O1、O2…On﹣1(內部有n﹣1個點),求∠BOn﹣1C(用n的代數式表示).
(4)如圖③,已知∠ABC、∠ACB的n等分線分別對應交于O1、O2…On﹣1,若∠BOn﹣1C=60°,求n的值.
【答案】(1)、115°;(2)、![]() ;(3)、﹣
;(3)、﹣![]() ×130°;(4)、n=13.
×130°;(4)、n=13.
【解析】
試題分析:(1)、△ABC中,已知∠A即可得到∠ABC與∠ACB的和,而BO、CO是∠ABC,∠ACB的兩條角平分線,即可求得∠OBC與∠OCB的度數,根據三角形的內角和定理即可求解;(2)、先根據三角形內角和定理求得∠ABC+∠ACB,再根據三等分線的定義求得∠O2BC+∠O2CB,即可求出∠BO2C;
(3)、先根據三角形內角和定理求得∠ABC+∠ACB,再根據n等分線的定義求得∠On﹣1BC+∠On﹣1CB,即可求出∠BOn﹣1C.(4)、依據(3)的結論即可求出n的值.
試題解析:(1)、∵△ABC中,∠ABC+∠ACB=180°﹣∠A=180°﹣50°=130°,BO、CO是∠ABC,∠ACB的兩條角平分線. ∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB, ∴∠OBC+∠OCB=
∠ACB, ∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=65°,
(∠ABC+∠ACB)=65°,
∴△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=115° (2)、∵點O2是∠ABC與∠ACB的三等分線的交點,
∴∠O2BC+∠O2CB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×130°=(
×130°=(![]() )°,
)°,
∴∠BO2C=180°﹣(![]() )°=(
)°=(![]() )°.
)°.
(3)、∵點On﹣1是∠ABC與∠ACB的n等分線的交點,
∴∠On﹣1BC+∠On﹣1CB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×130°, ∴∠BOn﹣1C=180°﹣
×130°, ∴∠BOn﹣1C=180°﹣![]() ×130°;
×130°;
(4)、∵∠BOn﹣1C=60°, ∴180°﹣![]() ×130°=60°,解得n=13.
×130°=60°,解得n=13.


科目:初中數學 來源: 題型:
【題目】(1)如圖(1),已知,在△ABC中,AD,AE分別是△ABC的高和角平分線,若∠B=30°,∠C=50°.求∠DAE的度數;
(2)如圖(2),已知AF平分∠BAC,交邊BC于點E,過F作FD⊥BC,若∠B=x°,∠C=(x+36)°,
①∠CAE= (含x的代數式表示)
②求∠F的度數.
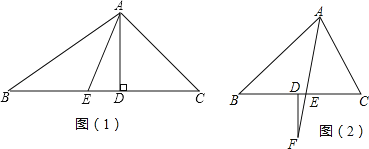
查看答案和解析>>
科目:初中數學 來源: 題型:
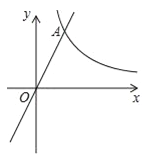
【題目】已知:如圖,在平面直角坐標系xOy中,反比例函數![]() 的圖象與正比例函數y=kx(k≠0)的圖象相交于橫坐標為2的點A,平移直線OA,使它經過點B(3,0),與y軸交于點C.
的圖象與正比例函數y=kx(k≠0)的圖象相交于橫坐標為2的點A,平移直線OA,使它經過點B(3,0),與y軸交于點C.
(1)求平移后直線的表達式;
(2)求∠OBC的余切值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列調查中,最適合采用全面調查(普查)方式的是( )
A. 對重慶市轄區(qū)內長江流域水質情況的調查
B. 對乘坐飛機的旅客是否攜帶違禁物品的調查
C. 對一個社區(qū)每天丟棄塑料袋數量的調查
D. 對重慶電視臺“天天630”欄目收視率的調查
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小亮和小瑩自制了一個標靶進行投標比賽,兩人各投了10次,如圖是他們投標成績的統計圖.
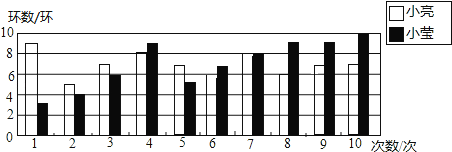
(1)根據圖中信息填寫下表
平均數 | 中位數 | 眾數 | |
小亮 | 7 | ||
小瑩 | 7 | 9 |
(2)分別用平均數和中位數解釋誰的成績比較好.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com