
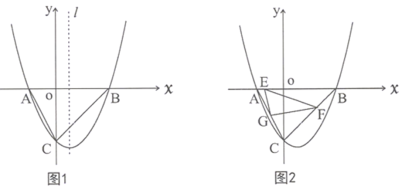
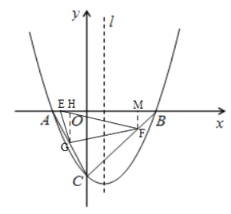
【題目】如圖1,已知拋物線![]() 與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C,且
與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C,且![]() .
.
(1)求該拋物線的函數表達式;
(2)設P是(1)中拋物線上的一個動點,當直線OC平分∠ACP時,求點P的坐標;
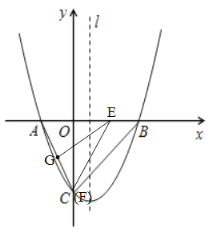
(3)如圖2,點G是線段AC的中點,動點E從點A出發,以每秒1個單位長度的速度向終點B運動,動點F從點B出發,以每秒![]() 個單位長度的速度向終點C運動,若E、F兩點同時出發,運動時間為t秒.則當t為何值時,
個單位長度的速度向終點C運動,若E、F兩點同時出發,運動時間為t秒.則當t為何值時,![]() 的面積是
的面積是![]() 的面積的
的面積的![]() ?
?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)當
;(3)當![]() 或
或![]()
【解析】
(1)根據OA、OB的長度求出點A、B的坐標,然后利用待定系數法求二次函數解析式解答;
(2)設![]() 與
與![]() 軸相交于點
軸相交于點![]() ,先求出C,D的坐標,再求出直線
,先求出C,D的坐標,再求出直線![]() 的解析式,聯立拋物線的函數表達式得出方程組,解方程組即可得點P的坐標;
的解析式,聯立拋物線的函數表達式得出方程組,解方程組即可得點P的坐標;
(3)先求出t的取值范圍,過點![]() 作
作![]() ⊥
⊥![]() 軸于點
軸于點![]() ,用t表示出BM的長度,然后用t表示出EH、HM、EM的長度,分兩種情況求出
,用t表示出BM的長度,然后用t表示出EH、HM、EM的長度,分兩種情況求出![]() 的面積,求出△ABC的面積,根據
的面積,求出△ABC的面積,根據![]() 的面積是
的面積是![]() 的面積的
的面積的![]() 列出關于t的方程,解方程即可求解.
列出關于t的方程,解方程即可求解.
解:(1)∵![]()
∴![]()
把![]() 分別代入
分別代入![]() 得:
得:
![]()
解得:![]()
∴![]()
(2)如圖,設![]() 與
與![]() 軸相交于點
軸相交于點![]()
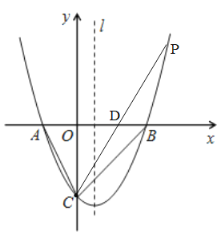
∵![]() 平分
平分![]() ,
,![]() ⊥
⊥![]()
∴![]()
∴![]()
把![]() 代入
代入![]() 得
得![]()
∴![]()
設直線![]() 的解析式為
的解析式為![]()
把![]() 分別代入
分別代入![]() 得
得
![]()
解得:![]()
∴![]()
依題意得
解得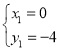 ,
,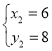
∴![]()
(3)如圖,過點![]() 作
作![]() ⊥
⊥![]() 軸于點
軸于點![]()
∵![]() ∥
∥![]() 軸
軸
∴![]() ∽
∽![]()
∴![]()
∴由![]()
得![]()
點![]() 運動到點
運動到點![]() 的時間為
的時間為![]() 秒,
秒,
點![]() 運動到點
運動到點![]() 的時間為
的時間為![]() 秒
秒
當![]() 時,如圖
時,如圖
過點![]() 作
作![]() ⊥
⊥![]() 軸于點
軸于點![]()
依題意得:![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
![]()
![]() 或
或![]()
∵![]()
![]() 的面積是
的面積是![]() 的面積的
的面積的![]()
∴![]() 或
或![]() =
=![]()
解得:![]() (舍去)或
(舍去)或![]() (舍去)
(舍去)
當![]() 時,如圖
時,如圖
![]()
![]()
![]()
∴![]()
綜上所述,當![]() 或
或![]() 時,
時,![]() 的面積是
的面積是![]() 的面積的
的面積的![]() .
.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:初中數學 來源: 題型:
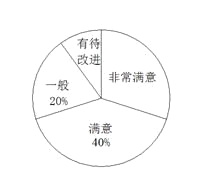
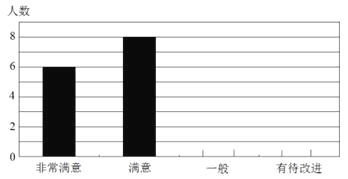
【題目】2012年4月5日下午,重慶一中初2013級“智力快車”比賽的決賽在渝北校區正式進行.“智力快車”活動是我校綜合實踐課程的傳統版塊,已有多年歷史,比賽試題的內容涉及到文史藝哲科技等多個方面.隨著時代的變化,其活動項目也在不斷更新.今年的比賽除了繼承傳統的“快速判斷”、“猜猜看”、“英語平臺”、“風險提速”四個環節外,特新增了“動手動腦”一項.比賽結束后,一綜合實踐小組成員就新增環節的滿意程度,對現場的觀眾進行了抽樣調查,給予評分,其中:非常滿意——5分,滿意——4分,一般——3分,有待改進——2分,并將調查結果制作成了如下的兩幅不完整的統計圖:

![]()
(1)本次共調查了 名同學,本次調查同學評分的平均得分為 分;
(2)將條形統計圖補充完整;
(3)如果評價為“一般”的只有一名是男生,評價為“有待改進”的只有一名是女生,
針對“動手動腦”環節的情況,綜合實踐小組的成員分別從評價為“一般”和評價
為“有待改進”的兩組中,分別隨機選出一名同學談談意見和建議,請你用列表或畫樹狀圖的方法求出所選兩名同學剛好都是女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
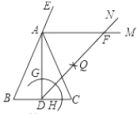
【題目】如圖,在△ABC中,AB=AC=6,BC=4,AD是BC邊上的高,AM是△ABC外角∠CAE的平分線.以點D為圓心,適當長為半徑畫弧,交DA于點G,交DC于點H.再分別以點G、H為圓心,大于![]() GH的長為半徑畫弧,兩弧在∠ADC內部交于點Q,連接DQ并延長與AM交于點F,則DF的長度為( ).
GH的長為半徑畫弧,兩弧在∠ADC內部交于點Q,連接DQ并延長與AM交于點F,則DF的長度為( ).
A.6B.![]() C.
C.![]() D.8
D.8
查看答案和解析>>
科目:初中數學 來源: 題型:
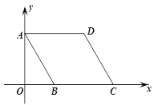
【題目】平面直角坐標系中,菱形ABCD如圖所示,![]() ,點D在線段AB的垂直平分線上,若菱形ABCD繞點O逆時針旋轉,旋轉速度為每秒
,點D在線段AB的垂直平分線上,若菱形ABCD繞點O逆時針旋轉,旋轉速度為每秒![]() ,則第70秒時點D的對應坐標為( )
,則第70秒時點D的對應坐標為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
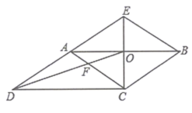
【題目】如圖,CE是平行四邊形ABCD的邊AB的垂直平分線,垂足為點![]() ,CE與DA的延長線交于點E,連接AC,BE,DO,DO與AC交于點F,則下列結論:①四邊形ACBE是菱形;②
,CE與DA的延長線交于點E,連接AC,BE,DO,DO與AC交于點F,則下列結論:①四邊形ACBE是菱形;②![]() ;③
;③![]() ;④S四邊形AFOE:
;④S四邊形AFOE:![]() ,其中正確的結論有( )
,其中正確的結論有( )
A.①②③B.①②④C.①②D.②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
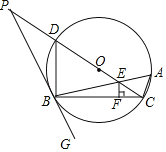
【題目】如圖,△ABC內接于⊙O,∠CBG=∠A,CD為直徑,OC與AB相交于點E,過點E作EF⊥BC,垂足為F,延長CD交GB的延長線于點P,連接BD.
(1)求證:PG與⊙O相切;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的條件下,若⊙O的半徑為8,PD=OD,求OE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
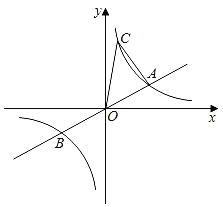
【題目】如圖,已知直線y=![]() x與雙曲線y=
x與雙曲線y=![]() (k>0)交于A、B兩點,A點的橫坐標為3,則下列結論:①k=6;②A點與B點關于原點O中心對稱;③關于x的不等式
(k>0)交于A、B兩點,A點的橫坐標為3,則下列結論:①k=6;②A點與B點關于原點O中心對稱;③關于x的不等式![]() <0的解集為x<﹣3或0<x<3;④若雙曲線y=
<0的解集為x<﹣3或0<x<3;④若雙曲線y=![]() (k>0)上有一點C的縱坐標為6,則△AOC的面積為8,其中正確結論的個數( )
(k>0)上有一點C的縱坐標為6,則△AOC的面積為8,其中正確結論的個數( )
A.4個B.3個C.2個D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
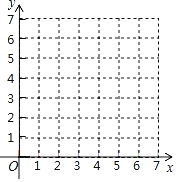
【題目】經過實驗獲得兩個變量x(x>0),y(y>0)的一組對應值如下表.
x | 1 | 2 | 3 | 4 | 5 | 6 |
y | 6 | 2.9 | 2 | 1.5 | 1.2 | 1 |
(1)請畫出相應函數的圖象,并求出函數表達式.
(2)點A(x1,y1),B(x2,y2)在此函數圖象上.若x1<x2,則y1,y2有怎樣的大小關系?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com