
【題目】如圖,已知拋物線y=ax2+bx+c(a≠0)的對稱軸是![]() ,且經過A(﹣4,0),C(0,2)兩點,直線l:y=kx+t(k≠0)經過A,C.
,且經過A(﹣4,0),C(0,2)兩點,直線l:y=kx+t(k≠0)經過A,C.
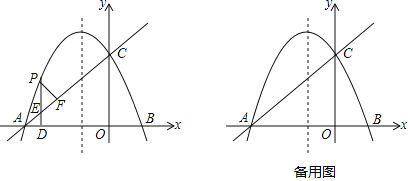
(1)求拋物線和直線l的解析式;
(2)點P是直線AC上方的拋物線上一個動點,過點P作PD⊥x軸于點D,交AC于點E,過點P作PF⊥AC,垂足為F,當△PEF≌△AED時,求出點P的坐標;
(3)在拋物線的對稱軸上是否存在點Q,使△ACQ為等腰三角形?若存在,直接寫出所有滿足條件的Q點的坐標;若不存在,請說明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)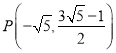 ;(3)存在,Q的坐標為:
;(3)存在,Q的坐標為: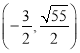 或
或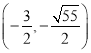
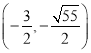 或
或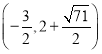 或
或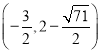 或
或![]() .
.
【解析】
(1)把點A、C的坐標和對稱軸表達式代入二次函數表達式,即可求解;
(2)PE![]() n2
n2![]() n+2
n+2![]() n﹣2,DE
n﹣2,DE![]() n+2,sin∠EAD=sin∠CAO,
n+2,sin∠EAD=sin∠CAO,![]() ,則AE
,則AE![]() DE
DE![]() (
(![]() n+2),當△PEF≌△AED時,PE=AE,
n+2),當△PEF≌△AED時,PE=AE,![]() n2﹣2n
n2﹣2n![]() (
(![]() n+2),即可求解;
n+2),即可求解;
(3)等腰三角形分A為頂角頂點、以C為頂角頂點、點Q為頂角頂點,三種情況分別求解即可.
(1)把點A、C的坐標和對稱軸表達式代入二次函數表達式得: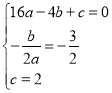 ,解得:
,解得: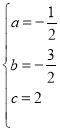 ,故拋物線的表達式為:y
,故拋物線的表達式為:y![]() x2
x2![]() x+2;
x+2;
同理把點A、C坐標代入直線l表達式并解得:y![]() x+2;
x+2;
(2)設P點坐標為(n,![]() n2
n2![]() n+2),∴E點坐標為(n,
n+2),∴E點坐標為(n,![]() n+2),∴PE
n+2),∴PE![]() n2
n2![]() n+2
n+2![]() n﹣2,DE
n﹣2,DE![]() n+2.
n+2.
∵A(﹣4,0),C(0,2),OA=4,OC=2,AC=2![]() .
.
∵PD⊥x軸于點D,∴∠ADE=90°,∴sin∠EAD=sin∠CAO,![]() ,∴AE
,∴AE![]() DE
DE![]() (
(![]() n+2),當△PEF≌△AED時,PE=AE,
n+2),當△PEF≌△AED時,PE=AE,![]() n2﹣2n
n2﹣2n![]() (
(![]() n+2),解得:n=﹣4或
n+2),解得:n=﹣4或![]() (舍去﹣4),∴n=
(舍去﹣4),∴n=![]() ,∴P(
,∴P(![]() ,
,![]() );
);
(3)存在,理由如下:
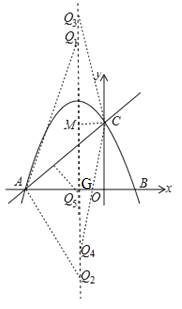
①以A為頂角頂點,AQ=AC,由(2)知AC=2![]() ,若設對稱軸與x軸交于點G,則AG
,若設對稱軸與x軸交于點G,則AG![]() (﹣4)
(﹣4)![]() ;
;
GQ1=GQ2![]() ,故點Q1、Q2的坐標分別為(
,故點Q1、Q2的坐標分別為(![]() ,
,![]() )、(
)、(![]() ,
,![]() );
);
②以C為頂角頂點,CQ=CA=2![]() ,過點C作x軸的平行線,交拋物線的對稱軸于點M,則M(
,過點C作x軸的平行線,交拋物線的對稱軸于點M,則M(![]() ,2),則CM
,2),則CM![]() ,MQ3
,MQ3![]() ,Q3G=2
,Q3G=2![]() ,Q4G=﹣2
,Q4G=﹣2![]() ,故Q3、Q4坐標分別為(
,故Q3、Q4坐標分別為(![]() ,2
,2![]() )、(
)、(![]() ,2
,2![]() );
);
③以點Q為頂角頂點時,同理可得點Q5(![]() ,0);
,0);
故點Q的坐標為:(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,2
,2![]() )或(
)或(![]() ,2
,2![]() )或(
)或(![]() ,0).
,0).


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2﹣2ax﹣2的圖象(記為拋物線C1)頂點為M,直線l:y=2x﹣a與x軸,y軸分別交于A,B.
(1)對于拋物線C1,以下結論正確的是 ;
①對稱軸是:直線x=1;②頂點坐標(1,﹣a﹣2);③拋物線一定經過兩個定點.
(2)當a>0時,設△ABM的面積為S,求S與a的函數關系;
(3)將二次函數y=ax2﹣2ax﹣2的圖象C1繞點P(t,﹣2)旋轉180°得到二次函數的圖象(記為拋物線C2),頂點為N.
①當﹣2≤x≤1時,旋轉前后的兩個二次函數y的值都會隨x的增大而減小,求t的取值范圍;
②當a=1時,點Q是拋物線C1上的一點,點Q在拋物線C2上的對應點為Q',試探究四邊形QMQ'N能否為正方形?若能,求出t的值,若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
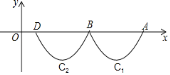
【題目】如圖,拋物線![]() 與x軸交于點A、B,把拋物線在x軸及其下方的部分記作C1,將C1向左平移得到C2,C2與x軸交于點B、D,若直線y=
與x軸交于點A、B,把拋物線在x軸及其下方的部分記作C1,將C1向左平移得到C2,C2與x軸交于點B、D,若直線y=![]() x+m與C1、C2共有3個不同的交點,則m的取值范圍是( )
x+m與C1、C2共有3個不同的交點,則m的取值范圍是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】鄭州市精準扶貧工作已進入攻堅階段.貧困戶張伯伯在相關單位的幫扶下把一片坡地改造后種植了優質水果藍莓,今年正式上市銷售在銷售的30天中,第一天賣出20千克為了擴大銷量采取了降價措施以后每天比前一天多賣出4千克第![]() 天的售價為
天的售價為![]() 元/千克,
元/千克,![]() 關于
關于![]() 的函數解析式為
的函數解析式為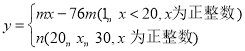 ,且第12天的售價為32元/千克,第26天的售價為25元/千克.已知種植銷售藍莓的成本是18元/千克,每天的利潤是
,且第12天的售價為32元/千克,第26天的售價為25元/千克.已知種植銷售藍莓的成本是18元/千克,每天的利潤是![]() 元(利潤=銷售收入
元(利潤=銷售收入![]() 成本).
成本).
(1)![]() _____________,
_____________,![]() ____________;
____________;
(2)求銷售藍莓第幾天時,當天的利潤最大?最大利潤是多少?
(3)在銷售藍莓的30天中,當天利潤不低于870元的共有多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,C是半圓O上一個動點,AB為半圓的直徑,D是弧BC的中點,過點D作半圓O的切線DE交AC的延長線于點E.
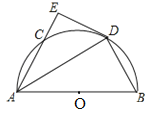
(1)求證:AE⊥DE;
(2)①已知CE=2,DE=4,則AB= ;
②連接OC,DC,當∠BAC= 度時,四邊形OBDC為菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形![]() 中,連接
中,連接![]() 點
點![]() 為
為![]() 上一點,使得
上一點,使得![]() 連接
連接![]() 交
交![]() 于點
于點![]() ,作
,作![]() 交
交![]() 的延長線于點
的延長線于點![]() .
.
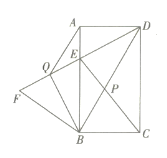
(1)求證:![]() .
.
(2)若![]() 求
求![]() 的長.
的長.
(3)在(2)的條件下,將![]() 沿著
沿著![]() 對折得到
對折得到![]() 點
點![]() 的對應點為點
的對應點為點![]() ,連接
,連接![]() 試求
試求![]() 的周長.
的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】快遞公司為提高快遞分揀的速度,決定購買機器人來代替人工分揀.已知購買甲型機器人1臺,乙型機器人2臺,共需14萬元;購買甲型機器人2臺,乙型機器人3臺,共需24萬元.
(1)求甲、乙兩種型號的機器人每臺的價格各是多少萬元;
(2)已知甲型和乙型機器人每臺每小時分揀快遞分別是1200件和1000件,該公司計劃購買這兩種型號的機器人共8臺,總費用不超過41萬元,并且使這8臺機器人每小時分揀快遞件數總和不少于8300件,則該公司有哪幾種購買方案?哪個方案費用最低,最低費用是多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
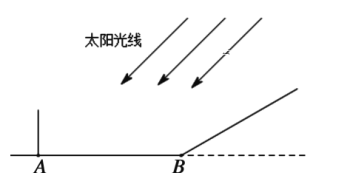
【題目】小芳身高1.6米,此時太陽光線與地面的夾角為45°.
(1)若小芳正站在水平地面A處上時,那么她的影長為多少米?
(2)若小芳來到一個坡度i=![]() 的坡面底端B處,當她在坡面上至少前進多少米時,小芳的影子恰好都落在坡面上?
的坡面底端B處,當她在坡面上至少前進多少米時,小芳的影子恰好都落在坡面上?
查看答案和解析>>
科目:初中數學 來源: 題型:
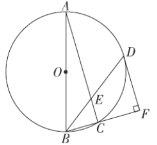
【題目】如圖,AB是⊙O的直徑,△ABC內接于⊙O.點D在⊙O 上,BD平分∠ABC交AC于點E,DF⊥BC交BC的延長線于點F.
(1)求證:FD是⊙O的切線;
(2)若BD=8,sin∠DBF=![]() ,求DE的長.
,求DE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com