
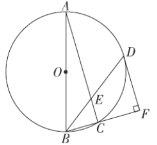
【題目】如圖,AB是⊙O的直徑,△ABC內接于⊙O.點D在⊙O 上,BD平分∠ABC交AC于點E,DF⊥BC交BC的延長線于點F.
(1)求證:FD是⊙O的切線;
(2)若BD=8,sin∠DBF=![]() ,求DE的長.
,求DE的長.
【答案】(1)詳見解析;(2)![]()
【解析】
(1)連接OD,根據角平分線的定義得到∠ABD=∠DBF,由等腰三角形的性質得到∠ABD=∠ODB,等量代換得到∠DBF=∠ODB,推出∠ODF=90°,根據切線的判定定理得到結論;
(2)連接AD,根據圓周角定理得到∠ADE=90°,根據角平分線的定義得到∠DBF=∠ABD,解直角三角形得到AD=6,在Rt△ADE中,解直角三角形得到DE=![]() .
.
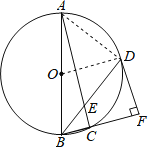
(1)連接OD,
∵BD平分∠ABC交AC于點E,
∴∠ABD=∠DBF,
∵OB=OD,
∴∠ABD=∠ODB,
∴∠DBF=∠ODB,
∵∠DBF+∠BDF=90°,
∴∠ODB+∠BDF=90°,
∴∠ODF=90°,
∴FD是⊙O的切線;
(2)連接AD,
∵AB是⊙O的直徑,
∴∠ADE=90°,
∵BD平分∠ABC交AC于點E,
∴∠DBF=∠ABD,
在Rt△ABD中,BD=8,
∵sin∠ABD=sin∠DBF=![]() ,
,
∴AB=10,AD=6,
∵∠DAC=∠DBC,
∴sin∠DAE=sin∠DBC=![]() ,
,
在Rt△ADE中,sin∠DAC=![]() ,
,
設DE=3x,則AE=5x,
∴AD=4x,
∴tan∠DAE=![]()
∴DE=![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c(a≠0)的對稱軸是![]() ,且經過A(﹣4,0),C(0,2)兩點,直線l:y=kx+t(k≠0)經過A,C.
,且經過A(﹣4,0),C(0,2)兩點,直線l:y=kx+t(k≠0)經過A,C.
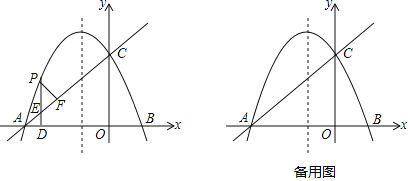
(1)求拋物線和直線l的解析式;
(2)點P是直線AC上方的拋物線上一個動點,過點P作PD⊥x軸于點D,交AC于點E,過點P作PF⊥AC,垂足為F,當△PEF≌△AED時,求出點P的坐標;
(3)在拋物線的對稱軸上是否存在點Q,使△ACQ為等腰三角形?若存在,直接寫出所有滿足條件的Q點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 、
、![]() 分別在邊
分別在邊![]() 、
、![]() 上,
上,![]() ,連結
,連結![]() ,點
,點![]() 、
、![]() 、
、![]() 分別為
分別為![]() 、
、![]() 、
、![]() 的中點.
的中點.

(1)觀察猜想圖1中,線段![]() 與
與![]() 的數量關系是_______,位置關系是_______;
的數量關系是_______,位置關系是_______;
(2)探究證明把![]() 繞點
繞點![]() 逆時針方向旋轉到圖2的位置,連結
逆時針方向旋轉到圖2的位置,連結![]() 、
、![]() 、
、![]() ,判斷
,判斷![]() 的形狀,并說明理由;
的形狀,并說明理由;
(3)拓展延伸把![]() 繞點
繞點![]() 在平面內自由旋轉,若
在平面內自由旋轉,若![]() ,
,![]() ,請直接寫出
,請直接寫出![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
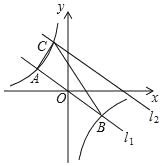
【題目】如圖,在平面直角坐標系中,直線l1:y=﹣![]() x與反比例函數y=
x與反比例函數y=![]() 的圖象交于A,B兩點(點A在點B左側),已知A點的縱坐標是2:
的圖象交于A,B兩點(點A在點B左側),已知A點的縱坐標是2:
(1)求反比例函數的表達式;
(2)將直線l1:y=﹣![]() x向上平移后的直線l2與反比例函數y=
x向上平移后的直線l2與反比例函數y=![]() 在第二象限內交于點C,如果△ABC的面積為30,求平移后的直線l2的函數表達式.
在第二象限內交于點C,如果△ABC的面積為30,求平移后的直線l2的函數表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上,且
上,且![]() ,以
,以![]() 為圓心,
為圓心,![]() 長為半徑作圓,
長為半徑作圓,![]() 經過點
經過點![]() ,與
,與![]() ,
,![]() 分別交于點
分別交于點![]() ,
,![]() .
.

(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)若![]() ,
,![]() ,求
,求![]() 的半徑;
的半徑;
(3)在(2)的條件下,若![]() 的內切圓圓心為
的內切圓圓心為![]() ,直接寫出
,直接寫出![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知點A(―3,6)、B(―9,一3),以原點O為位似中心,相似比為![]() ,把△ABO縮小,則點A的對應點A′的坐標是( )
,把△ABO縮小,則點A的對應點A′的坐標是( )

A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
查看答案和解析>>
科目:初中數學 來源: 題型:
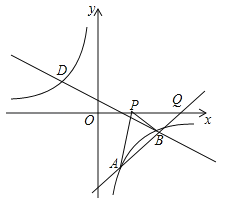
【題目】(2016湖北省黃岡市)如圖,已知點A(1,a)是反比例函數![]() 的圖象上一點,直線
的圖象上一點,直線![]() 與反比例函數
與反比例函數![]() 的圖象在第四象限的交點為點B.
的圖象在第四象限的交點為點B.
(1)求直線AB的解析式;
(2)動點P(x,0)在x軸的正半軸上運動,當線段PA與線段PB之差達到最大時,求點P的坐標.
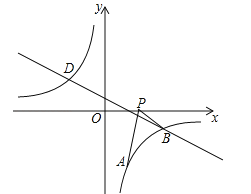
【答案】(1)y=x﹣4;(2)P(4,0).
【解析】試題分析:(1)先把A(1,a)代入反比例函數解析式求出a得到A點坐標,再解方程組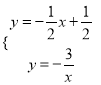 ,得B點坐標,然后利用待定系數法求AB的解析式;
,得B點坐標,然后利用待定系數法求AB的解析式;
(2)直線AB交x軸于點Q,如圖,利用x軸上點的坐標特征得到Q點坐標,則PA﹣PB≤AB(當P、A、B共線時取等號),于是可判斷當P點運動到Q點時,線段PA與線段PB之差達到最大,從而得到P點坐標.
試題解析:(1)把A(1,a)代入![]() 得a=﹣3,則A(1,﹣3),解方程組:
得a=﹣3,則A(1,﹣3),解方程組: 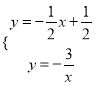 ,得:
,得: ![]() 或
或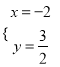 ,則B(3,﹣1),設直線AB的解析式為y=kx+b,把A(1,﹣3),B(3,﹣1)代入得:
,則B(3,﹣1),設直線AB的解析式為y=kx+b,把A(1,﹣3),B(3,﹣1)代入得: ![]() ,解得:
,解得: ![]() ,所以直線AB的解析式為y=x﹣4;
,所以直線AB的解析式為y=x﹣4;
(2)直線AB交x軸于點Q,如圖,當y=0時,x﹣4=0,解得x=4,則Q(4,0),因為PA﹣PB≤AB(當P、A、B共線時取等號),所以當P點運動到Q點時,線段PA與線段PB之差達到最大,此時P點坐標為(4,0).
考點:反比例函數與一次函數的交點問題.
【題型】解答題
【結束】
22
【題目】成都三圣鄉花卉基地出售兩種盆栽花卉:太陽花6元/盆,繡球花10元/盆.若一次購買的繡球花超過20盆時,超過20盆部分的繡球花價格打8折.
(1)若小張家花臺綠化需用60盆兩種盆栽花卉,小張爸爸給他460元錢去購買,問兩種花卉各買了多少盆?
(2)分別寫出兩種花卉的付款金額y(元)關于購買量x(盆)的函數解析式;
(3)為了美化環境,花園小區計劃到該基地購買這兩種花卉共90盆,其中太陽花數量不超過繡球花數量的一半.兩種花卉各買多少盆時,總費用最少,最少費用是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人在一條長為600m的筆直道路上均勻地跑步,速度分別為![]() 和
和![]() ,起跑前乙在起點,甲在乙前面50m處,若兩人同時起跑,則從起跑出發到其中一人先到達終點的過程中,兩人之間的距離y(m)與時間t(s)的函數圖象是( )
,起跑前乙在起點,甲在乙前面50m處,若兩人同時起跑,則從起跑出發到其中一人先到達終點的過程中,兩人之間的距離y(m)與時間t(s)的函數圖象是( )
A.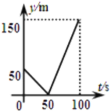 B.
B. C.
C.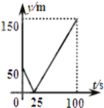 D.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com