
【題目】如圖,風車的支桿OE垂直于桌面,風車中心O到桌面的距離OE為25cm,小小風車在風吹動下繞著中心O不停地轉動,轉動過程中,葉片端點A、B、C、D在同一圓O上,已知⊙O的半徑為10cm,
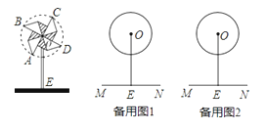
(1)風車在轉動過程中,當∠AOE=30°時,求點A到桌面的距離.
(2)在風車轉動一周的過程中,求點A相對于桌面的高度不超過20cm所經過的路線長.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)作A1F⊥MN于點F,A1G⊥OE于點G,在Rt△A1OG中,利用三角函數可求得OG,從而得出點A到桌面的距離A1F;
(2)作A2H⊥MN于H,則A2H=20cm,作A2D⊥OE于點D,則DE=A2H.在Rt△A2OD中,由特殊角的三角函數得∠A2OD=60°,由圓的軸對稱性可知,∠A3OA2=2∠A2OD=120°,從而得出點A所經過的路徑長.
解:(1)如圖(1),點A運動到點A1的位置時∠AOE=30°,作A1F⊥MN于點F,A1G⊥OE于點G,
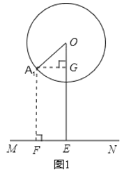
∴A1F=GE.
在Rt△A1OG中,
∵∠A1OG=30°,OA1=10cm,
∴OG=OA1cos30°=10×![]() cm.
cm.
∵OE=25 cm,
∴GE=OEOG=25![]() (cm),
(cm),
∴A1F=GE=25![]() (cm),
(cm),
答:點A到桌面的距離是25![]() 厘米;
厘米;
(2)如圖(2),點A在旋轉過程中運動到點A2、A3的位置時,點A到桌面的距離等于20厘米,作A2H⊥MN于H,則A2H=20 cm,作A2D⊥OE于點D,
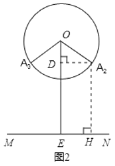
∴DE=A2H,
∵OE=25 cm,
∴OD=OEDE=2520=5 cm,
在Rt△A2OD中,OA2=10 cm,
∴cos∠A2OD=![]() ,
,
∴∠A2OD=60°.
由圓的對稱性可知,∠A3OA2=2∠A2OD=120°,
∴點A相對于桌面的高度不超過20cm所經過的路線長為:![]() cm.
cm.
答:點A相對于桌面的高度不超過20cm所經過的路線長為![]() 厘米.
厘米.


科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+bx+c(a>0)的對稱軸為x=-1,交x軸的一個交點為(x1,0),且0<x1<1, 則下列結論:①b>0,c<0;②a-b+c>0 ;③b<a ④ 3a+c>0,⑤9a-3b+c>0,其中正確的命題有( )個.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖的![]() 中,
中,![]() ,且
,且![]() 為
為![]() 上一點.今打算在
上一點.今打算在![]() 上找一點
上找一點![]() ,在
,在![]() 上找一點
上找一點![]() ,使得
,使得![]() 與
與![]() 全等,以下是甲、乙兩人的作法:
全等,以下是甲、乙兩人的作法:
(甲)連接![]() ,作
,作![]() 的中垂線分別交
的中垂線分別交![]() 、
、![]() 于
于![]() 點、
點、![]() 點,則
點,則![]() 、
、![]() 兩點即為所求
兩點即為所求
(乙)過![]() 作與
作與![]() 平行的直線交
平行的直線交![]() 于
于![]() 點,過
點,過![]() 作與
作與![]() 平行的直線交
平行的直線交![]() 于
于![]() 點,則
點,則![]() 、
、![]() 兩點即為所求
兩點即為所求
對于甲、乙兩人的作法,下列判斷何者正確?( )

A. 兩人皆正確B. 兩人皆錯誤
C. 甲正確,乙錯誤D. 甲錯誤,乙正確
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程![]() 。
。
(1)求證:方程有兩個不相等的實數根;
(2)若△ABC的兩邊AB、AC的長是方程的兩個實數根,第三邊BC的長為5。當△ABC是等腰三角形時,求k的值。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在□ABCD中,AB=2cm,線段AB與直線l之間的距離為![]() cm,線段CD的起始位置在MN處,此時∠MAB=1350,現將線段CD在直線l上向右移動,移動速度為1cm/s,運動時間為ts.
cm,線段CD的起始位置在MN處,此時∠MAB=1350,現將線段CD在直線l上向右移動,移動速度為1cm/s,運動時間為ts.
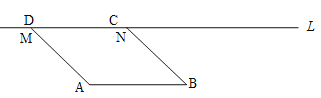
(1)當t=____s時,□ABCD為矩形;
(2)線段CD在直線l上移動過程中,當□ABCD為菱形時,求線段CD運動時間t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() .
.
(1)該拋物線的對稱軸是直線___________,頂點坐標是___________;
(2)選取適當的數據填入下表,并在圖中的直角坐標系內畫出該拋物線的圖像;


(3)根據圖像回答,![]() 有實數根,此時
有實數根,此時![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D為BC的中點,若動點E以1cm/s的速度從A點出發,沿著A→B→A的方向運動,設E點的運動時間為t秒(0≤t<6),連接DE,當△BDE是直角三角形時,t的值為
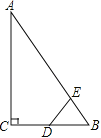
A、2 B、2.5或3.5 C、3.5或4.5 D、2或3.5或4.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀以下材料:
對數的創始人是蘇格蘭數學家納皮爾(J.Nplcr,1550﹣1617年),納皮爾發明對數是在指數書寫方式之前,直到18世紀瑞士數學家歐拉(Evlcr,1707﹣1783年)才發現指數與對數之間的聯系.
對數的定義:一般地,若![]() (
(![]() 且
且![]() ),那么
),那么![]() 叫做以
叫做以![]() 為底
為底![]() 的對數,記作
的對數,記作![]() ,比如指數式
,比如指數式![]() 可以轉化為對數式
可以轉化為對數式![]() ,對數式
,對數式![]() ,可以轉化為指數式
,可以轉化為指數式![]() .
.
我們根據對數的定義可得到對數的一個性質:
![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() ),理由如下:
),理由如下:
設![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
∴![]() ,由對數的定義得
,由對數的定義得![]()
又∵![]()
∴![]()
根據閱讀材料,解決以下問題:
(1)將指數式![]() 轉化為對數式________;
轉化為對數式________;
(2)求證:![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )
)
(3)拓展運用:計算![]() ________.
________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com