
【題目】如圖,拋物線y=ax2+bx+2交x軸于A(﹣1,0),B(4,0)兩點,交y軸于點C,與過點C且平行于x軸的直線交于另一點D,點P是拋物線上一動點.
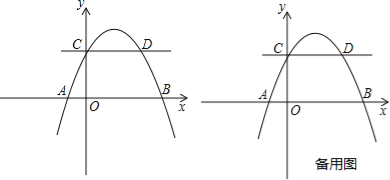
(1)求拋物線解析式及點D坐標;
(2)點E在x軸上,若以A,E,D,P為頂點的四邊形是平行四邊形,求此時點P的坐標;
(3)過點P作直線CD的垂線,垂足為Q,若將△CPQ沿CP翻折,點Q的對應點為Q′.是否存在點P,使Q′恰好落在x軸上?若存在,求出此時點P的坐標;若不存在,說明理由.
【答案】(1)![]() ,點D坐標為(3,2)(2)P1(0,2);P2(
,點D坐標為(3,2)(2)P1(0,2);P2(![]() ,﹣2);P3(
,﹣2);P3(![]() ,﹣2)(3)存在,(
,﹣2)(3)存在,(![]() ),(
),(![]() )
)
【解析】
解:(1)∵拋物線y=ax2+bx+2經過A(﹣1,0),B(4,0)兩點,
∴![]() ,解得:
,解得: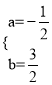 .
.
∴拋物線解析式為![]() .
.
當y=2時,![]() ,解得:x1=3,x2=0(舍去).
,解得:x1=3,x2=0(舍去).
∴點D坐標為(3,2).
(2)A,E兩點都在x軸上,AE有兩種可能:
①當AE為一邊時,AE∥PD,∴P1(0,2).
②當AE為對角線時,根據平行四邊形對頂點到另一條對角線距離相等,可知P點、D點到直線AE(即x軸)的距離相等,∴P點的縱坐標為﹣2.
代入拋物線的解析式:![]() ,解得:
,解得:![]() .
.
∴P點的坐標為(![]() ,﹣2),(
,﹣2),(![]() ,﹣2).
,﹣2).
綜上所述:P1(0,2);P2(![]() ,﹣2);P3(
,﹣2);P3(![]() ,﹣2).
,﹣2).
(3)存在滿足條件的點P,顯然點P在直線CD下方.
設直線PQ交x軸于F,點P的坐標為(![]() ),
),
①當P點在y軸右側時(如圖1),CQ=a,
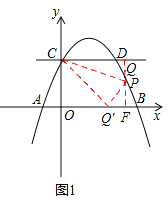
PQ=![]() .
.
又∵∠CQ′O+∠FQ′P=90°,∠COQ′=∠Q′FP=90°,
∴∠FQ′P=∠OCQ′,∴△COQ′∽△Q′FP,
∴![]() ,即
,即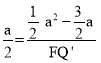 ,解得F Q′=a﹣3
,解得F Q′=a﹣3
∴OQ′=OF﹣F Q′=a﹣(a﹣3)=3,
![]() .
.
此時a=![]() ,點P的坐標為(
,點P的坐標為(![]() ).
).
②當P點在y軸左側時(如圖2)此時a<0,,![]() <0,CQ=﹣a,(無圖)
<0,CQ=﹣a,(無圖)
PQ=![]() .
.
又∵∠CQ′O+∠FQ′P=90°,∠CQ′O+∠OCQ′=90°,
∴∠FQ′P=∠OCQ′,∠COQ′=∠Q′FP=90°.
∴△COQ′∽△Q′FP.
∴![]() ,即
,即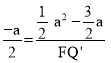 ,解得F Q′=3﹣a.
,解得F Q′=3﹣a.
∴OQ′=3,![]() .
.
此時a=﹣![]() ,點P的坐標為(
,點P的坐標為(![]() ).
).
綜上所述,滿足條件的點P坐標為(![]() ),(
),(![]() ).
).
(1)用待定系數法可得出拋物線的解析式,令y=2可得出點D的坐標.
(2)分兩種情況進行討論,①當AE為一邊時,AE∥PD,②當AE為對角線時,根據平行四邊形對頂點到另一條對角線距離相等,求解點P坐標.
(3)結合圖形可判斷出點P在直線CD下方,設點P的坐標為(![]() ),分情況討論,①當P點在y軸右側時,②當P點在y軸左側時,運用解直角三角形及相似三角形的性質進行求解即可.
),分情況討論,①當P點在y軸右側時,②當P點在y軸左側時,運用解直角三角形及相似三角形的性質進行求解即可.


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:初中數學 來源: 題型:
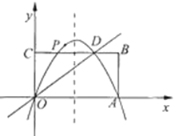
【題目】矩形OABC在直角坐標系中的位置如圖所示,A、C兩點的坐標分別為A(6,0)、C(0,3),直線y=![]() x與BC邊相交于D.
x與BC邊相交于D.
(1)求點D的坐標:
(2)若拋物線y=ax![]() +bx經過D、A兩點,試確定此拋物線的表達式:
+bx經過D、A兩點,試確定此拋物線的表達式:
(3)P為x軸上方(2)題中的拋物線上一點,求△POA面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
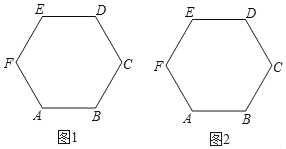
【題目】正六邊形ABCDEF的邊長1,請僅用無刻度的直尺按要求畫圖.
(1)在圖1中,畫出一條長度為![]() 的線段;
的線段;
(2)在圖2中,畫出一條長度為![]() 的線段,并說明理由.
的線段,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是半圓O的直徑,過點O作弦AD的垂線交半圓O于點E,交AC于點C,使∠BED=∠C.
(1)判斷直線AC與圓O的位置關系,并證明你的結論;
(2)若AC=8,cos∠BED=![]() ,求AD的長.
,求AD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年5月,以“尋根國學,傳承文明”為主題的蘭州市第三屆“國學少年強一國學知識挑戰賽”總決賽拉開帷幕,小明晉級了總決賽.比賽過程分兩個環節,參賽選手須在每個環節中各選擇一道題目.
第一環節:寫字注音、成語故事、國學常識、成語接龍(分別用![]() 表示);
表示);
第二環節:成語聽寫、詩詞對句、經典通讀(分別用![]() 表示)
表示)
(1)請用樹狀圖或列表的方法表示小明參加總決賽抽取題目的所有可能結果
(2)求小明參加總決賽抽取題目都是成語題目(成語故事、成語接龍、成語聽寫)的概率。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,函數![]() 的圖象G經過點
的圖象G經過點![]() ,直線
,直線![]() 與y軸交于點B,與圖象G交于點C.
與y軸交于點B,與圖象G交于點C.
(1)求m的值.
(2)橫、縱坐標都是整數的點叫做整點.記圖象G在點A,C之間的部分與線段BA,BC圍成的區域(不含邊界)為W.
①當直線l過點![]() 時,直接寫出區域W內的整點個數.
時,直接寫出區域W內的整點個數.
②若區域W內的整點不少于4個,結合函數圖象,求k的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
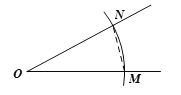
【題目】下面是小明設計的“已知兩線段及一角作三角形”的尺規作圖過程.
已知:線段![]() ,
,![]() 及∠O .
及∠O .

求作:△ABC,使得線段![]() ,
,![]() 及∠O分別是它的兩邊和一角.
及∠O分別是它的兩邊和一角.
作法:如圖,
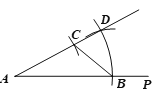
①以點O為圓心,![]() 長為半徑畫弧,分別交∠O的兩邊于點M ,N;
長為半徑畫弧,分別交∠O的兩邊于點M ,N;
②畫一條射線AP,以點A為圓心,![]() 長為半徑畫弧,交AP于點B;
長為半徑畫弧,交AP于點B;
③以點B為圓心,MN長為半徑畫弧,與第②步中所畫的弧相交于點D;
④畫射線AD;
⑤以點A為圓心,![]() 長為半徑畫弧,交AD于點C;
長為半徑畫弧,交AD于點C;
⑥連接BC ,則△ABC即為所求作的三角形.
請回答:
(1)步驟③得到兩條線段相等,即 = ;
(2)∠A=∠O的作圖依據是 ;
(3)小紅說小明的作圖不全面,原因是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,拋物線
中,拋物線![]() ﹔
﹔![]() 與
與![]() 軸交于點
軸交于點![]() ,拋物線
,拋物線![]() 的頂點為
的頂點為![]() ,直線
,直線![]() .
.
(1)當![]() 時,畫出直線
時,畫出直線![]() 和拋物線
和拋物線![]() ,并直接寫出直線
,并直接寫出直線![]() 被拋物線
被拋物線![]() 截得的線段長.
截得的線段長.
(2)隨著![]() 取值的變化,判斷點
取值的變化,判斷點![]() 是否都在直線
是否都在直線![]() 上并說明理由.
上并說明理由.
(3)若直線![]() 被拋物線
被拋物線![]() 截得的線段長不小于3,結合函數的圖像,直接寫出
截得的線段長不小于3,結合函數的圖像,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com