
【題目】如圖1,平面直角坐標系中,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于點
軸分別交于點![]() ,
,![]() ,直線
,直線![]() 經(jīng)過點
經(jīng)過點![]() ,并與
,并與![]() 軸交于點
軸交于點![]() .
.
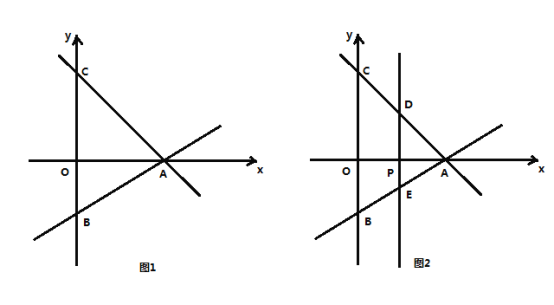
(1)求![]() ,
,![]() 兩點的坐標及
兩點的坐標及![]() 的值;
的值;
(2)如圖2,動點![]() 從原點
從原點![]() 出發(fā),以每秒
出發(fā),以每秒![]() 個單位長度的速度沿
個單位長度的速度沿![]() 軸正方向運動.過點
軸正方向運動.過點![]() 作
作![]() 軸的垂線,分別交直線
軸的垂線,分別交直線![]() ,
,![]() 于點
于點![]() ,
,![]() .設(shè)點
.設(shè)點![]() 運動的時間為
運動的時間為![]() .
.
①點![]() 的坐標為______.點
的坐標為______.點![]() 的坐標為_______;(均用含
的坐標為_______;(均用含![]() 的式子表示)
的式子表示)
②請從下面A、B兩題中任選一題作答我選擇________題.
A.當點![]() 在線段
在線段![]() 上時,探究是否存在某一時刻,使
上時,探究是否存在某一時刻,使![]() ?若存在,求出此時
?若存在,求出此時![]() 的面積;若不存在說明理由.
的面積;若不存在說明理由.
B.點![]() 是線段
是線段![]() 上一點.當點
上一點.當點![]() 在射線
在射線![]() 上時,探究是否存在某一時刻使
上時,探究是否存在某一時刻使![]() ?若存在、求出此時
?若存在、求出此時![]() 的值,并直接寫出此時
的值,并直接寫出此時![]() 為等腰三角形時點
為等腰三角形時點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
【答案】(1)點![]() 的坐標為
的坐標為![]() ,點B的坐標為
,點B的坐標為![]() ,
,![]() ;(2)①
;(2)①![]() ;
;![]() ;②A.
;②A.![]() ;B.點
;B.點![]() 的坐標為
的坐標為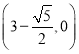 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根據(jù)一次函數(shù)與坐標軸的交點坐標特點即可求出![]() ,
,![]() 兩點的坐標,把
兩點的坐標,把![]() 點坐標代入
點坐標代入![]() 即可求出b;
即可求出b;
(2)①依題意得P(t,0),把x=t分別代入直線![]() ,
,![]() 即可表示出D,E的坐標;
即可表示出D,E的坐標;
②A,根據(jù)![]() =2,即可求出t,得到
=2,即可求出t,得到![]() ,利用
,利用![]() 即可求解;
即可求解;
B,分當點![]() 在線段
在線段![]() 上時和當點
上時和當點![]() 在線段
在線段![]() 的延長線上時分別表示出DE,根據(jù)
的延長線上時分別表示出DE,根據(jù)![]() 求出t,再根據(jù)等腰三角形的性質(zhì)即可求出
求出t,再根據(jù)等腰三角形的性質(zhì)即可求出![]() 點坐標.
點坐標.
(1)將![]() 代入
代入![]() 得
得![]() ,
,
解,得![]() ,
,
![]() 點
點![]() 的坐標為
的坐標為![]() .
.
將![]() 代入
代入![]() 得
得![]() ,
,
![]() 點B的坐標為
點B的坐標為![]() .
.
將![]() 代入
代入![]() ,得
,得![]()
解,得![]() .
.
(2)①依題意得P(t,0),把x=t分別代入直線![]() ,
,![]()
得 ![]() ;
;![]()
故答案為![]() ;
;![]() .
.
②A.由①得![]() ,
,![]() ,
,
![]() 點
點![]() 在線段
在線段![]() 上,
上,
![]() ,
,
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
解,得![]() .
.
![]() ,
,
![]() .
.
B.由①得![]() ,
,![]() .
.
![]() ,
,![]() .
.
當點![]() 在線段
在線段![]() 上時,
上時,
![]() ,
,
![]() ,
,
解得![]() .
.
∴P(3,0),D(3,1),E(3,-![]() )
)
設(shè)Q(a,0)(0≤a≤4)
故QD2=![]() ,QE2=
,QE2=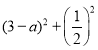 ,DE=
,DE=![]()
∵![]() 為等腰三角形
為等腰三角形
∴QD2=DE2或QE2=DE2
即![]() =
=![]() 或
或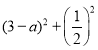 =
=![]()
解得a=![]() ,(a=
,(a=![]() 舍去)或a=
舍去)或a=![]() ,( a=
,( a=![]() 舍去)
舍去)
∴點![]() 的坐標為
的坐標為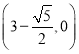 或
或![]() .
.
當點![]() 在線段
在線段![]() 的延長線上時,
的延長線上時,
![]()
![]() ,
,
解得![]() .
.
∴P(6,0),D(6,-2),E(6,1)
設(shè)Q(a,0)(0≤a≤4)
故QD2=![]() ,QE2=
,QE2=![]() ,DE=3
,DE=3
∵![]() 為等腰三角形
為等腰三角形
∴QD2=DE2或QE2=DE2
即![]() =9或
=9或![]() =9
=9
解得a=6-![]() ,(a=6+
,(a=6+![]() 舍去)或a=6-2
舍去)或a=6-2![]() ,( a=6+2
,( a=6+2![]() 舍去)
舍去)
點![]() 的坐標為
的坐標為![]() 或
或![]() .
.
綜上所述,點![]() 的坐標為
的坐標為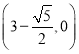 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】如圖所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,動點P從點A出發(fā)沿AD方向向點D以1cm/s的速度運動,動點Q從點C開始沿著CB方向向點B以3cm/s的速度運動.點P、Q分別從點A和點C同時出發(fā),當其中一點到達端點時,另一點隨之停止運動.
(1)經(jīng)過多長時間,四邊形PQCD是平行四邊形?
(2)經(jīng)過多長時間,四邊形PQBA是矩形?
(3)經(jīng)過多長時間,當PQ不平行于CD時,有PQ=CD.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,將Rt△AOB繞點O順時針旋轉(zhuǎn)90°后得到Rt△FOE,將線段EF繞點E逆時針旋轉(zhuǎn)90°后得到線段ED,分別以O、E為圓心,OA、ED長為半徑畫弧AF和弧DF,連接AD,則圖中陰影部分的面積是__.
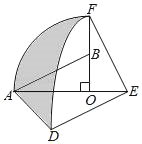
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在⊙O中,半徑OA與弦BD垂直,點C在⊙O上,∠AOB=80°
(1)若點C在優(yōu)弧BD上,求∠ACD的大小;
(2)若點C在劣弧BD上,直接寫出∠ACD的大小.
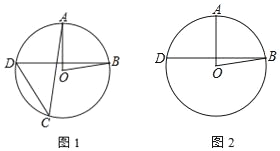
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
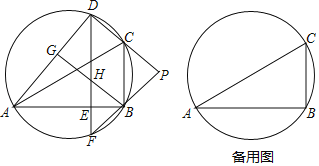
【題目】如圖,D是△ABC外接圓上的動點,且B,D位于AC的兩側(cè),DE⊥AB,垂足為E,DE的延長線交此圓于點F.BG⊥AD,垂足為G,BG交DE于點H,DC,F(xiàn)B的延長線交于點P,且PC=PB.
(1)求證:BG∥CD;
(2)設(shè)△ABC外接圓的圓心為O,若AB=![]() DH,∠OHD=80°,求∠BDE的大小.
DH,∠OHD=80°,求∠BDE的大小.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】風電已成為我國繼煤電、水電之后的第三大電源,風電機組主要由塔桿和葉片組成(如圖1),圖2是從圖1引出的平面圖.假設(shè)你站在A處測得塔桿頂端C的仰角是55°,沿HA方向水平前進43米到達山底G處,在山頂B處發(fā)現(xiàn)正好一葉片到達最高位置,此時測得葉片的頂端D(D、C、H在同一直線上)的仰角是45°.已知葉片的長度為35米(塔桿與葉片連接處的長度忽略不計),山高BG為10米,BG⊥HG,CH⊥AH,求塔桿CH的高.(參考數(shù)據(jù):tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,無人機在空中C處測得地面A、B兩點的俯角分別為60°、45°,如果無人機距地面高度CD為![]() 米,點A、D、E在同一水平直線上,則A、B兩點間的距離是_____米.(結(jié)果保留根號)
米,點A、D、E在同一水平直線上,則A、B兩點間的距離是_____米.(結(jié)果保留根號)

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
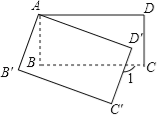
【題目】如圖,將矩形ABCD繞點A順時針旋轉(zhuǎn)到矩形AB′C′D′的位置,旋轉(zhuǎn)角為α(0°<α<90°),若∠1=110°,則∠α= .
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com