
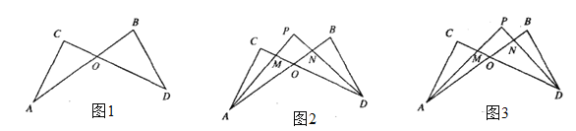
【題目】如圖1,線段AB、CD相交于點O,連結AC、BD,我們把形如圖1的圖形稱之為“8字形”,那么在這一個簡單的圖形中,到底隱藏了哪些數學知識呢?下面就請你發揮聰明才智,解決以下問題:
(1)在圖1中,請寫出∠A、∠B、∠C、∠D之間的數量關系,并說明理由;
(2)仔細觀察,在圖2中“8字形”的個數有 個;
(3)在圖2中,若∠B=70°,∠C=84°,∠CAB和∠BDC的平分線AP和DP相交于點P,并且與CD、AB分別相交于M、N利用(1)的結論,試求∠P的度數;
(4)在圖3中,如果∠B和∠C為任意角,并且AP和DP分別是∠CAB和∠BDC的四等分線,即∠PAO=![]() ∠CAO, ∠BDP=
∠CAO, ∠BDP=![]() ∠BDO,那么∠P與∠C、∠B之間存在的數量關系是 (直接寫出結論即可).
∠BDO,那么∠P與∠C、∠B之間存在的數量關系是 (直接寫出結論即可).
【答案】(1)∠A+∠C=∠D+∠B;(2)6;(3)77°;(4)![]()
【解析】
(1)根據三角形的內角和即可得到結論;
(2)以線段AC為邊的“8字型”有3個,以點O為交點的“8字型”有4個;
(3)根據角平分線的定義得到∠CAP=∠BAP,∠BDP=∠CDP,再根據三角形內角和定理得到∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,兩等式相減得到∠C-∠P=∠P-∠B,即∠P=![]() (∠C+∠B),然后把∠B=70°,∠C=84°代入計算即可;
(∠C+∠B),然后把∠B=70°,∠C=84°代入計算即可;
(4)同(3)的步驟可求出∠P與∠C、∠B之間存在的數量關系.
(1)∠A+∠C=∠D+∠B,
∵∠A+∠C+∠AOC=∠D+∠B+∠BOD=180°,
∠AOC=∠BOD,
∴∠A+∠C=∠D+∠B;
(2)交點有點M、N各有1個,交點O有4個,所以,“8字形”圖形共有6個;
(3)∵∠CAB和∠BDC的平分線AP和DP相交于點P,
∴∠CAP=∠BAP,∠BDP=∠CDP,
∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,
∴∠C-∠P=∠P-∠B,
即∠P=![]() (∠C+∠B),
(∠C+∠B),
∵∠C=84°,∠B=70°
∴∠P=![]() (∠C+∠B)=
(∠C+∠B)=![]() (84°+70°)=77°.
(84°+70°)=77°.
(4) ∵∠PAO=![]() ∠CAO, ∠BDP=
∠CAO, ∠BDP=![]() ∠BDO,
∠BDO,
∴∠PAC=![]() ∠CAO, ∠ODP=
∠CAO, ∠ODP=![]() ∠BDO,
∠BDO,
∵∠CAP+∠C=∠ODP+∠P,∠BAP+∠P=∠BDP+∠B,
∴![]() ∠CAO +∠C=
∠CAO +∠C=![]() ∠BDO +∠P,
∠BDO +∠P,![]() ∠CAO +∠P=
∠CAO +∠P=![]() ∠BDO +∠B,
∠BDO +∠B,
∴![]() ∠CAO +3∠P=
∠CAO +3∠P=![]() ∠BDO +3∠B,
∠BDO +3∠B,
∴∠C-3∠P=∠P-3∠B,
∴![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】將一根24cm的筷子置于底面直徑為8cm,高為15cm的圓柱形水杯中,如圖所示,設筷子露在杯子外面的長度為hcm,則h的取值范圍是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A在O正北方向,B在O正東方向,且A、B到點O的距離相等,甲從A出發,以每小時60千米的速度朝正東方向行駛,乙從B出發,以每小時40千米的速度朝正北方向行駛,1小時后,位于點O處的觀察員發現甲乙兩人之間的夾角為45°,此時甲乙兩人相距( )千米。

A. 80 B. 50![]() C. 100
C. 100![]() D. 100
D. 100
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(8分)如圖,四邊形ABCD為正方形,點A的坐標為(0,1),點B的坐標為(0,﹣2),反比例函數![]() 的圖象經過點C,一次函數
的圖象經過點C,一次函數![]() 的圖象經過A、C兩點.
的圖象經過A、C兩點.

(1)求反比例函數與一次函數的解析式;
(2)求反比例函數與一次函數的另一個交點M的坐標;
(3)若點P是反比例函數圖象上的一點,△OAP的面積恰好等于正方形ABCD的面積,求P點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,將一副直角三角板放在同一條直線AB上,其中∠ONM=30°,∠OCD=45°.
(1)將圖1中的三角板OMN繞點O按逆時針方向旋轉,使∠BON=30°,如圖2,MN與CD相交于點E,求∠CEN的度數;
(2)將圖1中的三角尺OMN繞點O按每秒20°的速度沿逆時針方向旋轉一周,在旋轉的過程中,求在第幾秒時,邊MN恰好與邊CD平行?(友情提醒:先畫出符合題意的圖形,然后再探究)
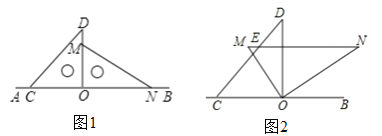
查看答案和解析>>
科目:初中數學 來源: 題型:
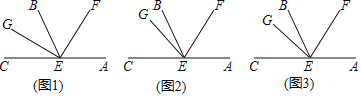
【題目】如圖,E是直線AC上一點,EF是∠AEB的平分線.
(1)如圖1,若EG是∠BEC的平分線,求∠GEF的度數;
(2)如圖2,若GE在∠BEC內,且∠CEG=3∠BEG,∠GEF=75°,求∠BEG的度數.
(3)如圖3,若GE在∠BEC內,且∠CEG=n∠BEG,∠GEF=α,求∠BEG(用含n、α的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為提高居民的節水意識,向陽小區開展了“建設節水型社區,保障用水安全”為主題的節水宣傳活動,小瑩同學積極參與小區的宣傳活動,并對小區300戶家庭用水情況進行了抽樣調查,她在300戶家庭中,隨機調查了50戶家庭5月份的用水量情況,結果如圖所示.

(1)試估計該小區5月份用水量不高于12 t的戶數占小區總戶數的百分比;
(2)把圖中每組用水量的值用該組的中間值(如0~6的中間值為3)來替代,估計該小區5月份的用水量.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖①、圖②、圖③都是由邊長為1的小等邊三角形構成的網格,每個小等邊三角形的頂點稱為格點.線段AB的端點在格點上.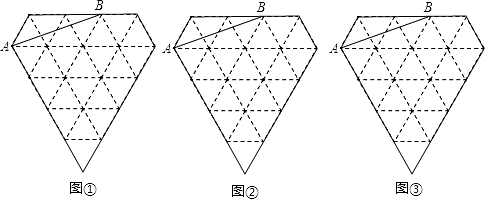
(1)在圖①、圖2中,以AB為邊各畫一個等腰三角形,且第三個頂點在格點上;(所畫圖形不全等)
(2)在圖③中,以AB為邊畫一個平行四邊形,且另外兩個頂點在格點上.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,點E是BC上一點,直線AE交BD于點M,交DC的延長線于點F,G是EF的中點,連接CG.求證:
(1)△ABM≌△CBM;
(2)CG⊥CM.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com