
【題目】![]() 中,
中,![]() ,
,![]() 為高線,點
為高線,點![]() 在邊
在邊![]() 上,且
上,且![]() ,連接
,連接![]() ,
,![]() ,與邊
,與邊![]() 相交于點
相交于點![]() .
.
(1)如圖1,當![]() 時,求證:
時,求證:![]()
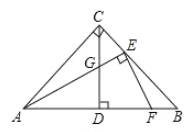
(2)如圖2,當![]() 時,則線段
時,則線段![]() 、
、![]() 的數量關系為 ;
的數量關系為 ;
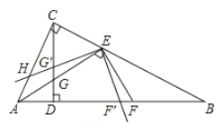
(3)如圖3,在(2)的條件下,將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() ,旋轉后
,旋轉后![]() 邊所在的直線與邊
邊所在的直線與邊![]() 相交于點
相交于點![]() ,
,![]() 邊所在的直線與邊
邊所在的直線與邊![]() 相交于點
相交于點![]() ,與高線
,與高線![]() 相交于點
相交于點![]() ,若
,若![]() ,且
,且![]() ,求線段
,求線段![]() H的長.
H的長.
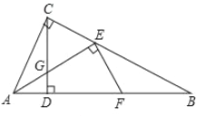
【答案】(1)證明見解析;(2)當![]() 時,
時,![]() ;(3)2
;(3)2![]()
【解析】
(1)根據tan∠BAC=1=tan45°,得出△ABC為等腰直角三角形,再過E點作EK⊥BC,EK與CD相交于點K,得出∠GKE=45°=∠B,再根據∠GEK+∠KEF=90°=∠KEF+∠BEF,得出△GEK∽△FEB,從而證出![]() ,即可得出EF=2EG;
,即可得出EF=2EG;
(2)根據(1)的證明過程,同理可證出當tan∠BAC=2時,得出EF=EG;
(3)根據(2)的結論,先設AC=3k,得出BC=6k,EC=![]() EC=2k,再過點E作EM⊥BC,EM與CD的延長線相交于點M,得出△AGC∽△EGM,得出
EC=2k,再過點E作EM⊥BC,EM與CD的延長線相交于點M,得出△AGC∽△EGM,得出![]() ,再過點G作GN∥EH,與AH相交于點N,得出△ANG∽△AHE,得出NH的值,同理得出△GEM∽△FEB,得出EF=EG.同理可證EF′=EG′,∠FEF'=∠GEG',得出△GEG'≌△FEF',即可證出
,再過點G作GN∥EH,與AH相交于點N,得出△ANG∽△AHE,得出NH的值,同理得出△GEM∽△FEB,得出EF=EG.同理可證EF′=EG′,∠FEF'=∠GEG',得出△GEG'≌△FEF',即可證出![]() 的值,再根據HG′∥NG,同理可證
的值,再根據HG′∥NG,同理可證![]() ,得出EC=CH,得出△HCE是等腰直角三角形,在△HG'C中,求出CW的值,從而得出G′H的值.
,得出EC=CH,得出△HCE是等腰直角三角形,在△HG'C中,求出CW的值,從而得出G′H的值.
(1)證明:在![]() 中,
中, ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 為等腰直角三角形,
為等腰直角三角形,
![]() ,
,
![]() ,
,
過![]() 點作
點作![]() ,
,![]() 與
與![]() 相交于點
相交于點![]() ,
,
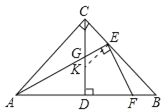
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)根據(1)的證明,同理可證:
當![]() 時,
時,![]() ;
;
(3)在![]() 中,
中, ![]() ,
,![]() ,
,
則![]() ,
,
設![]() ,則BC=6k,則
,則BC=6k,則![]() ,
,
過點![]() 作
作![]() ,
,![]() 與
與![]() 的延長線相交于點
的延長線相交于點![]() ,
, ![]() ,
,
![]() .
.
在 過點 同理可證 在 設![]() 與
與![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 作
作![]() ,與
,與![]() 相交于點
相交于點![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() ,同理可證
,同理可證![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() 中,過點
中,過點![]() 作
作![]() ,垂足是
,垂足是![]() ,
,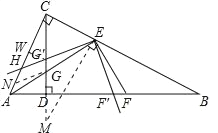
![]() ,則HW=x,則
,則HW=x,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.


 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:初中數學 來源: 題型:
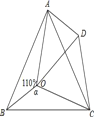
【題目】如圖,點O是等邊△ABC內一點,∠AOB=110°,∠BOC=α,將△BOC繞點C按順時針方向旋轉60°得△ADC,連接OD,得△AOD,若△AOD為等腰三角形,則α=________
查看答案和解析>>
科目:初中數學 來源: 題型:
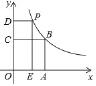
【題目】如圖,在平面直角坐標系中,面積為4的正方形![]() 的頂點
的頂點![]() 與坐標原點重合,邊
與坐標原點重合,邊![]() 、
、![]() 分別在
分別在![]() 軸、
軸、![]() 軸的正半軸上,點
軸的正半軸上,點![]() 、
、![]() 都在函數
都在函數![]() 的圖象上,過動點
的圖象上,過動點![]() 分別作
分別作![]() 軸、
軸、![]() 軸的平行線,交
軸的平行線,交![]() 軸、
軸、![]() 軸于點
軸于點![]() 、
、![]() .設矩形
.設矩形![]() 與正方形
與正方形![]() 重疊部分圖形的面積為
重疊部分圖形的面積為![]() ,點
,點![]() 的橫坐標為m.
的橫坐標為m.
(1)求![]() 的值;
的值;
(2)用含![]() 的代數式表示
的代數式表示![]() 的長;
的長;
(3)求![]() 與
與![]() 之間的函數關系式.
之間的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于平面直角坐標系xOy中的![]() 和點P,給出如下定義:如果在
和點P,給出如下定義:如果在![]() 上存在一個動點Q,使得
上存在一個動點Q,使得![]() 是以CQ為底的等腰三角形,且滿足底角
是以CQ為底的等腰三角形,且滿足底角![]() ,那么就稱點P為
,那么就稱點P為![]() 的“關聯點”.
的“關聯點”.
![]() 當
當![]() 的半徑為2時,
的半徑為2時,
![]() 在點
在點![]() ,
,![]() ,
,![]() 中,
中,![]() 的“關聯點”是______;
的“關聯點”是______;
![]() 如果點P在射線
如果點P在射線![]() 上,且P是
上,且P是![]() 的“關聯點”,求點P的橫坐標m的取值范圍.
的“關聯點”,求點P的橫坐標m的取值范圍.
![]() 的圓心C在x軸上,半徑為4,直線
的圓心C在x軸上,半徑為4,直線![]() 與兩坐標軸交于A和B,如果線段AB上的點都是
與兩坐標軸交于A和B,如果線段AB上的點都是![]() 的“關聯點”,直接寫出圓心C的橫坐標n的取值范圍.
的“關聯點”,直接寫出圓心C的橫坐標n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2018年大唐芙蓉園新春燈會以“鼓舞中華”為主題,既有新年韻味,又結合“一帶一路”展示了絲綢之路上古今文化經貿繁榮的盛況。小麗的爸爸買了兩張門票,她和各個兩人都想去觀看,可是爸爸只能帶一人去,于是讀九年級的哥哥提議用他們3人吃飯的彩色筷子做游戲(筷子除顏色不同,其余均相同),其中小麗的筷子顏色是紅色,哥哥的是銀色,爸爸的是白色,將3人的3雙款子全部放在 一個不透明的筷簍里搖勻,小麗隨機從筷簍里取出一根,記下顏色放回,然后哥哥同樣從筷簍里取出一根,若兩人取出的筷子顏色相同則小麗去,若不同,則哥哥去。
(1)求小麗隨機取出一根筷子是紅色的概率;
(2)請用列表或畫樹狀圖的方法求出小隨爸爸去看新春燈會的概率。
查看答案和解析>>
科目:初中數學 來源: 題型:
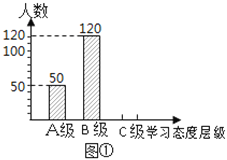
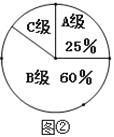
【題目】某市教育局對該市部分學校的八年級學生對待學習的態度進行了一次抽樣調查(把學習態度分為三個層級,A級:對學習很感興趣;B級:對學習較感興趣;C級:對學習不感興趣),并將調查結果繪制成圖①和圖②的統計圖(不完整).請根據圖中提供的信息,解答下列問題:
(1)此次抽樣調查中,共調查了________名學生;
(2)圖②中C級所占的圓心角的度數是__________;
(3)根據抽樣調查結果,請你估計該市近20000名八年級學生中大約有多少名學生學習態度達標(達標包括A級和B級)?
查看答案和解析>>
科目:初中數學 來源: 題型:
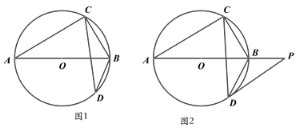
【題目】已知AB是⊙O的的直徑,弦CD與AB相交,∠BCD=25°。
(1)如圖1,求∠ABD的大小;
(2)如圖2,過點D作O的切線,與AB的延長線交于點P,若DP∥AC,求∠OCD的度數。
查看答案和解析>>
科目:初中數學 來源: 題型:
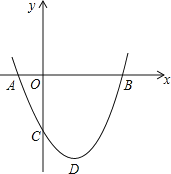
【題目】如圖,二次函數![]() 圖象的頂點為D,其圖象與x軸的交點A、B的橫坐標分別為
圖象的頂點為D,其圖象與x軸的交點A、B的橫坐標分別為![]() ,
,![]() 與y軸負半軸交于點C.
與y軸負半軸交于點C.
![]() 若
若![]() 是等腰直角三角形,求a的值.
是等腰直角三角形,求a的值.
![]() 探究:是否存在a,使得
探究:是否存在a,使得![]() 是等腰三角形?若存在,求出符合條件的a的值;不存在,說明理由.
是等腰三角形?若存在,求出符合條件的a的值;不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com