
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 是斜邊上一點,且
是斜邊上一點,且![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)過點![]() 的
的![]() 與邊
與邊![]() 相切,切點為
相切,切點為![]() 的中點
的中點![]() ,
,![]() 與直線
與直線![]() 的另一個交點為
的另一個交點為![]() .
.
(i)求![]() 的半徑;
的半徑;
(ⅱ)連接![]() ,試探究
,試探究![]() 與
與![]() 的位置關(guān)系,并說明理由.
的位置關(guān)系,并說明理由.
【答案】(Ⅰ)tan∠BCD=![]() ;(Ⅱ)(i)
;(Ⅱ)(i)![]() ;(ⅱ)AF⊥CD,理由見解析.
;(ⅱ)AF⊥CD,理由見解析.
【解析】
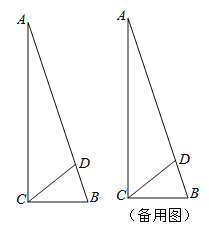
(Ⅰ)如圖1,過D作DM⊥BC,垂足M,則DM∥AC,可得△DMB∽△ACB,根據(jù)相似三角形的性質(zhì)即可求出DM和CM的長,進一步即可求出結(jié)果;
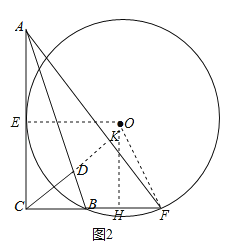
(Ⅱ)(ⅰ)如圖2,連接OE,OF,根據(jù)切線的性質(zhì)得到OE⊥AC,作OH⊥BE,垂足為H,則四邊形OHCE為矩形,于是可得OH的長,設(shè)⊙O的半徑為r,則可根據(jù)垂徑定理和矩形的性質(zhì)用r的代數(shù)式表示出HF的長,然后在Rt△OHF中根據(jù)勾股定理即可建立關(guān)于r的方程,解方程即得結(jié)果;
(ⅱ)如圖2,延長CD,交AF于點K,先由(ⅰ)的結(jié)果求出CF的長,進一步即可求出tan∠CAF的值,與(Ⅰ)題的結(jié)果對比可得∠CAF=∠BCD,進而可根據(jù)直角三角形的性質(zhì)和等量代換得出∠FCK+∠AFC=90°,于是可得結(jié)論.
解:(Ⅰ)如圖1,過D作DM⊥BC,垂足M,
∵∠ACB=90°,
∴DM∥AC.
∴△DMB∽△ACB,
∵AD=4BD,AC=3,BC=1,
∴DM=![]() AC=
AC=![]() ,CM=
,CM=![]() BC=
BC=![]() .
.
則在Rt△DMC中,tan∠DCM=![]() ,
,
即tan∠BCD=![]() ;
;

(Ⅱ)(ⅰ)如圖2,連接OE,OF,
∵⊙O與AC相切于AC中點E,
∴OE⊥AC,
作OH⊥BC,垂足為H,∵∠ACB=90°,
∴四邊形OHCE為矩形,
設(shè)⊙O的半徑為r,則OF=OE=CH=r,
∴OH=CE=![]() AC=
AC=![]() ,HF=BH=CH﹣BC=r﹣1.
,HF=BH=CH﹣BC=r﹣1.
∴在Rt△OHF中,由勾股定理得:OF2=OH2+HF2,
∴r2=![]() +(r﹣1)2,
+(r﹣1)2,
解得r=![]() ;
;
(ⅱ) AF與CD的位置關(guān)系是AF⊥CD,理由如下:
如圖2,延長CD,交AF于點K,
由(ⅰ)知,CF=BC+BF=1+2(r﹣1)=![]() ,
,
∴在Rt△ACF中,∠ACB=90°,tan∠CAF=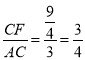 ,
,
∵tan∠BCD=![]() ,
,
∴∠CAF=∠BCD,即∠CAF=∠FCK,
∵∠CAF+∠AFC=90°,
∴∠FCK+∠AFC=90°.
即AF⊥CD.


科目:初中數(shù)學 來源: 題型:
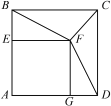
【題目】如圖,正方形AEFG的頂點E、G在正方形ABCD的邊AB、AD上,連接BF、DF.
![]() (1)求證:BF=DF;
(1)求證:BF=DF;
(2)連接CF,請直接寫出![]() 的值為__________(不必寫出計算過程).
的值為__________(不必寫出計算過程).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
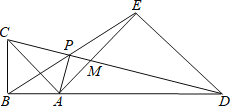
【題目】如圖,點A在線段BD上,在BD的同側(cè)作等腰Rt△ABC和等腰Rt△ADE,其中∠ABC=∠AED=90°,CD與BE、AE分別交于點P、M.對于下列結(jié)論:①△CAM∽△DEM;②CD=2BE;③MPMD=MAME;④2CB2=CPCM.其中正確的是( )
A. ①②B. ①②③C. ①②③④D. ①③④
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
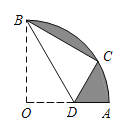
【題目】如圖,在扇形AOB中,∠AOB=90°,半徑OA=4.將扇形AOB沿過點B的直線折疊,點O恰好落在弧AB上點C處,折痕交OA于點D,則圖中陰影部分的面積為_______ .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】觀察下列等式,探究發(fā)現(xiàn)規(guī)律,并解決問題,
①![]() ;
;
②![]() ;
;
③![]() ;
;
(1)直接寫出第④個等式: ;
(2)猜想第![]() 個等式(用含字母
個等式(用含字母![]() 的式子表示),并說明這個等式的正確性;
的式子表示),并說明這個等式的正確性;
(3)利用發(fā)現(xiàn)的規(guī)律,求![]() 的值.(參考數(shù)據(jù):
的值.(參考數(shù)據(jù):![]() )
)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
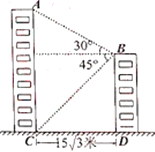
【題目】如圖,某校教學樓![]() 與實驗樓
與實驗樓![]() 的水平間距
的水平間距![]() 米,在實驗樓頂部
米,在實驗樓頂部![]() 點測得教學樓頂部
點測得教學樓頂部![]() 點的仰角是
點的仰角是![]() ,底部
,底部![]() 點的俯角是
點的俯角是![]() ,則教學樓
,則教學樓![]() 的高度是____米(結(jié)果保留根號).
的高度是____米(結(jié)果保留根號).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,直線a∥b,∠1=40°,∠2=80°,則∠3的度數(shù)為( )
[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/15/2485292109684736/2491850430775296/STEM/0502255e02c3498e9234cb6eaef26eb9.png]
A.120°B.130°C.140°D.110°
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
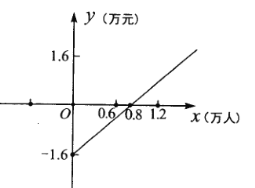
【題目】某公共汽車線路每天運營毛利潤![]() (萬元)與乘客量
(萬元)與乘客量![]() (萬人)成一次函數(shù)關(guān)系,其圖象如圖所示.目前通過監(jiān)測發(fā)現(xiàn)每天平均乘客量為0.6萬人次,由于運營成本較高,這條線路處于虧損狀態(tài).(毛利潤=票價總收入一運營成本)
(萬人)成一次函數(shù)關(guān)系,其圖象如圖所示.目前通過監(jiān)測發(fā)現(xiàn)每天平均乘客量為0.6萬人次,由于運營成本較高,這條線路處于虧損狀態(tài).(毛利潤=票價總收入一運營成本)
(1)求該線路公共汽車的單程票價和每天運營成本分別為多少元.
(2)公交公司為了扭虧,若要使每天運營毛利潤在0.2~0.4萬元之間(包括0.2和0.4),求平均每天的乘客量![]() 的范圍.
的范圍.
(3)據(jù)實際情況,發(fā)現(xiàn)該線路乘客量穩(wěn)定,公交公司決定適當提高票價,當單程票價每提高1元時,每天平均乘客量相應(yīng)減少0.05萬人次,設(shè)這條線路的單程票價提高![]() 元(
元(![]() ).當
).當![]() 為何值時,該線路每天運營總利潤最大,并求出最大的總利潤.
為何值時,該線路每天運營總利潤最大,并求出最大的總利潤.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com