
【題目】已知如圖,在矩形ABCD中,AB=4cm,BC=7cm,
(1)點F在邊BC上,且 BF=3,若點P從點A出發,以每秒1cm的速度沿A→D→C→F運動,設點P運動的時間為t秒,求當t為何值時,△AFP為等腰三角形?




(2)如圖2,將長方形ABCD折疊,折痕為MN,點A的對應點A′落在線段BC上,當點A′ 在BC上移動時,點M、N也隨之移動,若限定點M、N分別在線段AB、AD上移動,則點A′ 在線段BC上可移動的最大距離是___________.

【答案】(1)5s,6s,8s,![]() s;(2)(
s;(2)(![]() -3)cm;
-3)cm;
【解析】
(1)利用輔助圓確定點P的位置,再利用等腰三角形的性質判定定理分別確定點P的運動路程,即可得到運動時間;
(2)利用M,N的運動位置確定A′的最大運動位置即可;
解:(1)①如圖,以A為圓心,AF長為半徑畫圓,交AD于![]() ,則AF=A
,則AF=A![]()
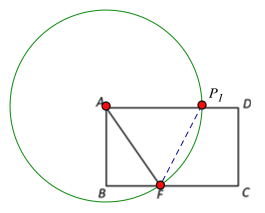
在Rt△ABF中,AB=4cm,BF=3cm,
∴AF=![]() =5cm;
=5cm;
∴AP1=AF=5cm;
∴t1=5s;
∴當t1=5s時,
②如圖,以F為圓心,AF長為半徑畫圓,交AD于![]() ,則FA=F
,則FA=F![]() ,交DC于
,交DC于![]() ,則FA=F
,則FA=F![]()
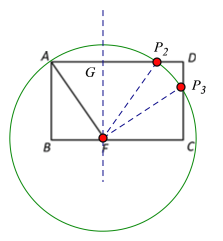
∵BF=3cm, AB=4cm,
∴FA=![]() =5cm;
=5cm;
∴FP2=FP3=FA=5cm,
作FG⊥AD于G,則AP2=2AG=2BF=6cm,
∴t2=6s;
又∵BC=7cm,
∴FC=7-3=4cm,
∴CP3=![]() =3cm,
=3cm,
∴DP3=1cm,
∴AD+DP3=8cm,
∴t3=8s;
③作AF的垂直平分線,交AD于![]() ,交AF于H,連接F
,交AF于H,連接F![]()

∵ABCD為矩形,
∴AD∥BC,∠B=90°,
∴∠DAF=∠AFB,
又∠AHP4=∠B=90°,
∴△AHP4∽△ABF,
![]() ,
,
∴AP4=![]() ,
,
∴t4=![]() s;
s;
綜上,當t=5s,6s,8s,![]() s時,△AFP為等腰三角形。
s時,△AFP為等腰三角形。
(2)如圖, 當點M與點D重合時, 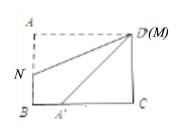
根據翻折對稱性可得:DA′=DA=7cm,
在Rt△A′CD中,
A′C=![]() =
=![]() cm,
cm,
如圖,當點N與點B重合時,

根據翻折對稱性可得BA′=AB=4cm.
∵A′C=CB-BA′,
∴A′C=3cm.
∴點A′在BC邊上可移動的最大距離為(![]() -3)cm.
-3)cm.


 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:初中數學 來源: 題型:
【題目】某村耕地總面積為50公頃,且該村人均耕地面積y(單位:公頃/人)與總人口x(單位:人)的函數圖象如圖所示,則下列說法正確的是( ) 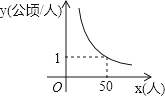
A.該村人均耕地面積隨總人口的增多而增多
B.該村人均耕地面積y與總人口x成正比例
C.若該村人均耕地面積為2公頃,則總人口有100人
D.當該村總人口為50人時,人均耕地面積為1公頃
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=ax2+bx+c的圖象如圖所示,則一次函數y=ax+b與反比例函數y= ![]() 在同一平面直角坐標系內的圖象大致為( )
在同一平面直角坐標系內的圖象大致為( ) 
A.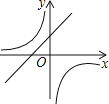
B.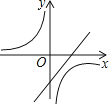
C.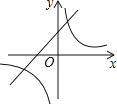
D.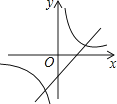
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在如圖的正方形網格中,每一個小正方形的邊長為1.格點三角形![]() (頂點是網格線交點的三角形)的頂點
(頂點是網格線交點的三角形)的頂點![]() 的坐標分別是
的坐標分別是![]() .
.
(1)請在圖中的網格平面內建立平面直角坐標系;
(2)請畫出![]() 關于
關于![]() 軸對稱的
軸對稱的![]() ;
;
(3)請在![]() 軸上求作一點
軸上求作一點![]() ,使
,使![]() 的周長最小,并寫出點
的周長最小,并寫出點![]() 的坐標.
的坐標.
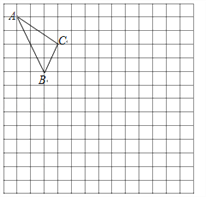
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AD是△ABC的角平分線,DF⊥AB,垂足為F,DE=DG,△ADG和△AED的面積分別為40和28,則△EDF的面積為( )

A. 12 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角墻角AOB(OA⊥OB,且OA、OB長度不限)中,要砌20m長的墻,與直角墻角AOB圍成地面為矩形的儲倉,且地面矩形AOBC的面積為96m2 . 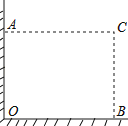
(1)求這地面矩形的長;
(2)有規格為0.80×0.80和1.00×1.00(單位:m)的地板磚單價分別為55元/塊和80元/塊,若只選其中一種地板磚都恰好能鋪滿儲倉的矩形地面(不計縫隙),用哪一種規格的地板磚費用較少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在等邊三角形ABC中,點P在△ABC內,點Q在△ABC外,且∠ABP=∠ACQ, BP=CQ.
(1)求證:△ABP≌△ACQ;
(2)請判斷△APQ是什么形狀的三角形?試說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是二次函數y=ax2+bx+c圖象的一部分,圖象過點A(﹣3,0),對稱軸為直線x=﹣1,下列給出四個結論中,正確結論的個數是( )個
①c>0;
②若點B(﹣ ![]() ,y1)、C(﹣
,y1)、C(﹣ ![]() ,y2)為函數圖象上的兩點,則y1<y2;
,y2)為函數圖象上的兩點,則y1<y2;
③2a﹣b=0;
④ ![]() <0;
<0;
⑤4a﹣2b+c>0.
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知等邊△ABC的高為6,在這個三角形所在的平面內有一點P,若點P到直線AB的距離是1,點P到直線AC的距離是3,則點P到直線BC的距離可能是_______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com