
【題目】如圖,在平面直角坐標系中.頂點為(﹣4,﹣1)的拋物線交y軸于點A(0,3),交x軸于B,C兩點.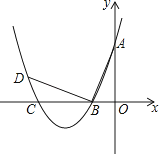
(1)求此拋物線的解析式;
(2)已知點P是拋物線上位于B,C兩點之間的一個動點,問:當點P運動到什么位置時,四邊形ABPC的面積最大?并求出此時四邊形ABPC的面積.
(3)過點B作AB的垂線交拋物線于點D,是否存在以點C為圓心且與線段BD和拋物線的對稱軸l同時相切的圓?若存在,求出圓的半徑;若不存在,請說明理由.
【答案】
(1)
【解答】解:根據題意,可設拋物線的解析式為y=a(x+4)2﹣1,
把點A(0,3)代入得:3=16a﹣1,
解得a=![]() ,
,
所以此拋物線的解析式為y=![]() (x+4)2﹣1;
(x+4)2﹣1;
(2)
令y=0,則0=![]() (x+4)2﹣1;
(x+4)2﹣1;
解得x1=﹣2,x2=﹣6,
∴B(﹣2,0),C(﹣6,0),
∴BC=4,
∵S四邊形ABPC=S△ABC+S△PBC,S△ABC=![]() BCOA=
BCOA=![]() ×4×3=6,
×4×3=6,
∴要使四邊形ABPC的面積最大,則△PBC的面積最大,
∴當P點移動到拋物線的頂點時△PBC的面積最大,
∴四邊形ABPC的面積的最大值為:S△ABC+S△PBC=6+![]() ×4×1=6+2=8;
×4×1=6+2=8;
(3)
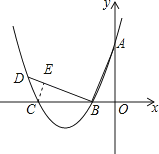
如圖,設⊙C與BD相切于點E,連接CE,則∠BEC=∠AOB=90°.
∵A(0,3)、B(﹣2,0)、C(﹣6,0),
∴OA=3,OB=2,OC=6,BC=4;
∴AB=![]() =
=![]() ,
,
∵AB⊥BD,
∴∠ABC=∠EBC+90°=∠OAB+90°,
∴∠EBC=∠OAB,
∴△OAB∽△EBC,
∴![]() ,即
,即![]()
∴EC=![]() .
.
設拋物線對稱軸交x軸于F.
∵拋物線的對稱軸x=﹣4,
∴CF=2≠![]() ,
,
∴不存在以點C為圓心且與線段BD和拋物線的對稱軸l同時相切的圓.
【解析】


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,A為某旅游景區的最佳觀景點,游客可從B處乘坐纜車先到達小觀景平臺DE觀景,然后再由E處繼續乘坐纜車到達A處,返程時從A處乘坐升降電梯直接到達C處,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(參考數據:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在水平地面上豎立著一面墻AB,墻外有一盞路燈D.光線DC恰好通過墻的最高點B,且與地面形成37°角.墻在燈光下的影子為線段AC,并測得AC=5.5米.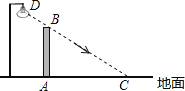
(1)求墻AB的高度(結果精確到0.1米);(參考數據:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80)
(2)如果要縮短影子AC的長度,同時不能改變墻的高度和位置,請你寫出兩種不同的方法
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現在的青少年由于沉迷電視、手機、網絡游戲等,視力日漸減退,某市為了解學生的視力變化情況,從全市九年級隨機抽取了1500名學生,統計了每個人連續三年視力檢查的結果,根據視力在4.9以下的人數變化制成折線統計圖,并對視力下降的主要因素進行調查,制成扇形統計圖.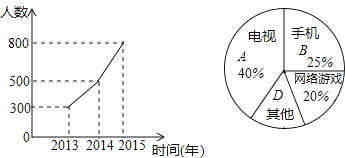
解答下列問題:
(1)圖中D所在扇形的圓心角度數為 ;
(2)若2015年全市共有30000名九年級學生,請你估計視力在4.9以下的學生約有多少名?
(3)根據扇形統計圖信息,你覺得中學生應該如何保護視力?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:(1)2﹣1﹣![]() tan60°+(π﹣2015)0+|﹣
tan60°+(π﹣2015)0+|﹣![]() |;
|;
解方程:(2)x2﹣1=2(x+1).
(1)計算:2﹣1﹣![]() tan60°+(π﹣2015)0+|﹣
tan60°+(π﹣2015)0+|﹣![]() |;
|;
(2)解方程:x2﹣1=2(x+1).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=3,BC=5,點P是BC邊上的一個動點(點P與點B、C都不重合),現將△PCD沿直線PD折疊,使點C落到點F處;過點P作∠BPF的角平分線交AB于點E.設BP=x,BE=y,則下列圖象中,能表示y與x的函數關系的圖象大致是( )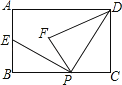
A.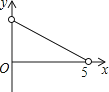
B.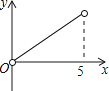
C.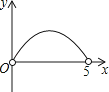
D.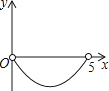
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】理解:數學興趣小組在探究如何求tan15°的值,經過思考、討論、交流,得到以下思路:
思路一 如圖1,在Rt△ABC中,∠C=90°,∠ABC=30°,延長CB至點D,使BD=BA,連接AD.設AC=1,則BD=BA=2,BC=![]() .tanD=tan15°=
.tanD=tan15°=![]() =
=![]() =2﹣
=2﹣![]() .
.
思路二 利用科普書上的和(差)角正切公式:tan(α±β)=![]() .假設α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=
.假設α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=![]() =
=![]() =2﹣
=2﹣![]() .
.
思路三 在頂角為30°的等腰三角形中,作腰上的高也可以…
思路四 …
請解決下列問題(上述思路僅供參考).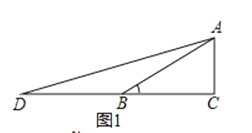
(1)類比:求出tan75°的值;
(2)應用:如圖2,某電視塔建在一座小山上,山高BC為30米,在地平面上有一點A,測得A,C兩點間距離為60米,從A測得電視塔的視角(∠CAD)為45°,求這座電視塔CD的高度;
(3)拓展:如圖3,直線y=![]() x﹣1與雙曲線y=
x﹣1與雙曲線y=![]() 交于A,B兩點,與y軸交于點C,將直線AB繞點C旋轉45°后,是否仍與雙曲線相交?若能,求出交點P的坐標;若不能,請說明理由.
交于A,B兩點,與y軸交于點C,將直線AB繞點C旋轉45°后,是否仍與雙曲線相交?若能,求出交點P的坐標;若不能,請說明理由.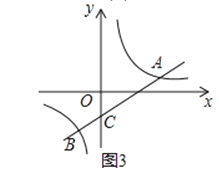
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C、D分別在扇形AOB的半徑OA、OB的延長線上,且OA=3,AC=3 ![]() ﹣3,CD∥AB,并與弧AB相交于點M、N.
﹣3,CD∥AB,并與弧AB相交于點M、N. 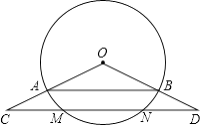
(1)求線段OD的長;
(2)若sin∠C= ![]() ,求弦MN的長;
,求弦MN的長;
(3)在(2)的條件下,求優弧MEN的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com