
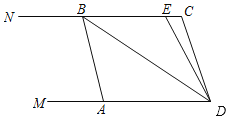
【題目】如圖,已知兩條直線DM∥CN,線段AB的兩個端點A、B分別在直線OM、CN上,∠C=∠BAD,點E在線段BC上,且DB平分∠ADE.
(1)求證:AB∥CD;
(2)若沿著NC方向平移線段AB,那么∠CBD與∠CED度數之間的關系是否隨著AB位置的變化而變化?若變化,請找出變化規律;若不變化,請確定它們之間的數量關系.
科目:初中數學 來源: 題型:
【題目】已知一張三角形紙片![]() 如圖甲
如圖甲![]() ,其中
,其中![]() 將紙片沿過點B的直線折疊,使點C落到AB邊上的E點處,折痕為
將紙片沿過點B的直線折疊,使點C落到AB邊上的E點處,折痕為![]() 如圖乙
如圖乙![]() 再將紙片沿過點E的直線折疊,點A恰好與點D重合,折痕為
再將紙片沿過點E的直線折疊,點A恰好與點D重合,折痕為![]() 如圖丙
如圖丙![]() 原三角形紙片ABC中,
原三角形紙片ABC中,![]() 的大小為______
的大小為______![]()

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知a是最大的負整數,b、c滿足![]() ,且a,b,c分別是點A,B,C在數軸上對應的數.
,且a,b,c分別是點A,B,C在數軸上對應的數.
(1)求a,b,c的值,并在數軸上標出點A,B,C;
![]()
(2)若動點P從C出發沿數軸正方向運動,點P的速度是每秒2個單位長度,運動幾秒后,點P到達B點?
(3)在數軸上找一點M,使點M到A,B,C三點的距離之和等于13,請直接寫出所有點M對應的數.(不必說明理由)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在△ABC中,BA=BC,BD是△ABC的中線,△ABC的角平分線AE交BD于點F,過點C作AB的平行線交AE的延長線于點G
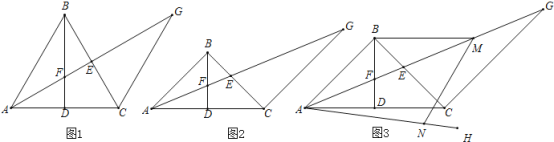
(1)如圖1,若∠ABC=60°,求證:AF=![]() EG;
EG;
(2)如圖2,若∠ABC=90°,求證:AF=![]() EG;
EG;
(3)在(2)的條件下如圖3,過點A作∠CAH=![]() ∠FAC,過點B作BM∥AC交AG于點M,點N在AH上,連接MN、BN,若∠BMN+∠EAH=90°,
∠FAC,過點B作BM∥AC交AG于點M,點N在AH上,連接MN、BN,若∠BMN+∠EAH=90°,![]() ,求BN的長.
,求BN的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】春季是傳染病多發的季節,積極預防傳染病是學校高度重視的一項工作,為此,某校對學生宿舍采取噴灑藥物進行消毒.在對某宿舍進行消毒的過程中,先經過![]() 的集中藥物噴灑,再封閉宿舍
的集中藥物噴灑,再封閉宿舍![]() ,然后打開門窗進行通風,室內每立方米空氣中含藥量
,然后打開門窗進行通風,室內每立方米空氣中含藥量![]() 與藥物在空氣中的持續時間
與藥物在空氣中的持續時間![]() 之間的函數關系,在打開門窗通風前分別滿足兩個一次函數,在通風后又成反比例,如圖所示.下面四個選項中錯誤的是( )
之間的函數關系,在打開門窗通風前分別滿足兩個一次函數,在通風后又成反比例,如圖所示.下面四個選項中錯誤的是( )
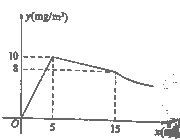
A. 經過![]() 集中噴灑藥物,室內空氣中的含藥量最高達到
集中噴灑藥物,室內空氣中的含藥量最高達到![]()
B. 室內空氣中的含藥量不低于![]() 的持續時間達到了
的持續時間達到了![]()
C. 當室內空氣中的含藥量不低于![]() 且持續時間不低于35分鐘,才能有效殺滅某種傳染病毒.此次消毒完全有效
且持續時間不低于35分鐘,才能有效殺滅某種傳染病毒.此次消毒完全有效
D. 當室內空氣中的含藥量低于![]() 時,對人體才是安全的,所以從室內空氣中的含藥量達到
時,對人體才是安全的,所以從室內空氣中的含藥量達到![]() 開始,需經過
開始,需經過![]() 后,學生才能進入室內
后,學生才能進入室內
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點M為直線AB上一動點, ![]() 都是等邊三角形,連接BN
都是等邊三角形,連接BN
![]() 求證:
求證: ![]() ;
;
![]() 分別寫出點M在如圖2和圖3所示位置時,線段AB、BM、BN三者之間的數量關系
分別寫出點M在如圖2和圖3所示位置時,線段AB、BM、BN三者之間的數量關系![]() 不需證明
不需證明![]() ;
;
![]() 如圖4,當
如圖4,當![]() 時,證明:
時,證明: ![]() .
.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com