
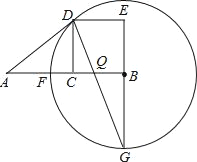
【題目】設C為線段AB的中點,四邊形BCDE是以BC為一邊的正方形.以B為圓心,BD長為半徑的⊙B與AB相交于F點,延長EB交⊙B于G點,連接DG交于AB于Q點,連接AD.
求證:(1)AD是⊙B的切線;(2)AD=AQ;(3)BC2=CFEG.
【答案】(1)證明見解析;(2)證明見解析;(3)證明見解析.
【解析】試題分析:(1)連接BD,由DC⊥AB,C為AB的中點,由線段垂直平分線的性質,可得AD=BD,再根據正方形的性質,可得∠ADB=90°;
(2)由BD=BG與CD∥BE,利用等邊對等角與平行線的性質,即可求得∠G=∠CDG=∠BDG=![]() ∠BCD=22.5°,繼而求得∠ADQ=∠AQD=67.5°,由等角對等邊,可證得AD=AQ;
∠BCD=22.5°,繼而求得∠ADQ=∠AQD=67.5°,由等角對等邊,可證得AD=AQ;
(3)易求得∠GDE=∠GDB+∠BDE=67.5°=∠DFE,∠DCF=∠E=90°,即可證得Rt△DCF∽Rt△GED,根據相似三角形的對應邊成比例,即可證得結論.
試題解析:
(1)連接BD,
∵四邊形BCDE是正方形,
∴∠DBA=45°,∠DCB=90°,即DC⊥AB,
∵C為AB的中點,
∴CD是線段AB的垂直平分線,
∴AD=BD,
∴∠DAB=∠DBA=45°,
∴∠ADB=90°,
即BD⊥AD,
∵BD為半徑,
∴AD是⊙B的切線;
(2)∵BD=BG,
∴∠BDG=∠G,
∵CD∥BE,
∴∠CDG=∠G,
∴∠G=∠CDG=∠BDG=![]() ∠BCD=22.5°,
∠BCD=22.5°,
∴∠ADQ=90°﹣∠BDG=67.5°,∠AQB=∠BQG=90°﹣∠G=67.5°,
∴∠ADQ=∠AQD,
∴AD=AQ;
(3)連接DF,
在△BDF中,BD=BF,
∴∠BFD=∠BDF,
又∵∠DBF=45°,
∴∠BFD=∠BDF=67.5°,
∵∠GDB=22.5°,
在Rt△DEF與Rt△GCD中,
∵∠GDE=∠GDB+∠BDE=67.5°=∠DFE,∠DCF=∠E=90°,
∴Rt△DCF∽Rt△GED,
∴![]() ,
,
又∵CD=DE=BC,
∴BC2=CFEG.



 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】將正整數按如圖所示的規律排列下去,若用有序數對(m,n)表示從上到下第m排,從左到右第n個數,如(4,2)表示整數8.則(62,55)表示的數是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在北海市創建全國文明城活動中,需要30名志愿者擔任“講文明樹新風”公益廣告宣傳工作,其中男生18人,女生12人.
(1)若從這30人中隨機選取一人作為“展板掛圖”講解員,求選到女生的概率;
(2)若“廣告策劃”只在甲、乙兩人中選一人,他們準備以游戲的方式決定由誰擔任,游戲規則如下:將四張牌面數字分別為2,3,4,5的撲克牌洗勻后,數字朝下放于桌面,從中任取2張,若牌面數字之和為偶數,則甲擔任,否則乙擔任.試問這個游戲公平嗎?請用樹狀圖或列表法說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小李對初三(1)班全體同學的業余興趣愛好(第一愛好)進行了一次調查,她根據采集到的數據,繪制了下面的圖1和圖2.

請你根據圖中提供的信息,解答下列問題:
(1)初三(1)班共有學生________人;
(2)在圖1中,將“書畫”部分的圖形補充完整;
(3)在圖2中,“球類”部分所對應的圓心角的度數________度;愛好“音樂”的人數占本班學生數的百分數是________;愛好“書畫”的人數占本班學生數的百分數是________;“其它”的人數占本班學生數的百分數是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明學習了《有理數》后,對運算非常感興趣,于是定義了一種新運算“△”規則如下:對于兩個有理數m , n , m △ n =![]() .
.
(1)計算:1△(-2)= ;
(2)判斷這種新運算是否具有交換律,并說明理由;
(3)若a![]() =| x-1| , a
=| x-1| , a![]() =| x-2|,求a
=| x-2|,求a![]() △ a
△ a ![]() (用含 x 的式子表示)
(用含 x 的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】按要求完成下列視圖問題:
(1)如圖(1),它是由6個同樣大小的正方體擺成的幾何體,將正方體①移走后,新幾何體從三個方向看到的圖形與原幾何體從三個方向看到的圖形相比,從 方向看到的形狀圖沒有發生改變?
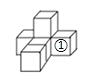
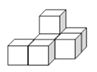
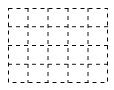
(2)如圖(2),請你在右側虛線網格圖a中畫出該幾何體從上面看到的形狀圖
(3)如圖(3),它是由幾個小立方塊組成從上面看到的形狀圖,小正方形上的數字表示該位置上的正方體的個數,請你在右側建線網格圖b中面出該幾何體從正面看到的形狀圖.
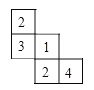
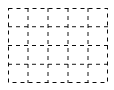
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在抗洪搶險中,人民解放軍的沖鋒舟沿東西方向的河流搶救災民,早晨從![]() 地出發,晚上最后到達
地出發,晚上最后到達![]() 地,約定向東為正方向,當天航行依次記錄如下(單位:千米)
地,約定向東為正方向,當天航行依次記錄如下(單位:千米)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,問:
,問:
(1)![]() 地在
地在![]() 地的東面,還是西面?與
地的東面,還是西面?與![]() 地相距多少千米?
地相距多少千米?
(2)這一天沖鋒舟離![]() 最遠多少千米?
最遠多少千米?
(3)若沖鋒舟每千米耗油![]() 升,郵箱容量為
升,郵箱容量為![]() 升,求途中至少需要補充多少升油?
升,求途中至少需要補充多少升油?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形![]() 中,
中,![]() ,點
,點![]() 為邊
為邊![]() 上一點,連接
上一點,連接![]() 交對角線
交對角線![]() 于點
于點![]() .
.
(1)如圖1,已知![]() 于
于![]() ,菱形的邊長為6,求線段
,菱形的邊長為6,求線段![]() 的長度;
的長度;
(2)如圖2,已知點![]() 為邊
為邊![]() 上一點,連接
上一點,連接![]() 交線段
交線段![]() 于點
于點![]() ,且滿足
,且滿足![]() ,
,![]() ,求證:
,求證:![]() .
.
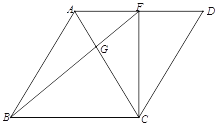
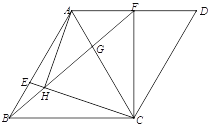
圖1 圖2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀:能夠成為直角三角形三條邊長的三個正整數a,b,c,稱為勾股數.世界上第一次給出勾股數通解公式的是我國古代數學著作《九章算術》,其勾股數組公式為: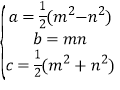 其中m>n>0,m,n是互質的奇數.
其中m>n>0,m,n是互質的奇數.
應用:當n=1時,求有一邊長為5的直角三角形的另外兩條邊長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com